Cho hình vẽ sau với \(\widehat {{D_1}} = \widehat {{D_2}}\). Chọn câu sai.

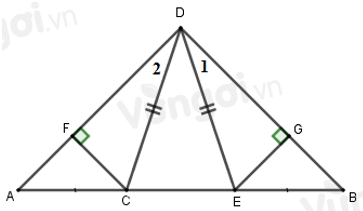
Vì tam giác \(CDE\) cân tại \(D\) (do \(DC = DE\)) nên \(\widehat {DCE} = \widehat {DEC}\)  (tính chất tam giác cân)   (1)

Lại có \(\widehat {DCA} + \widehat {DCE} = 180^\circ \) và \(\widehat {DEB} + \widehat {DEC} = 180^\circ \) (hai góc kề bù)

Suy ra \(\widehat {DCA} = 180^\circ  - \widehat {DCE}\); \(\widehat {DEB} = 180^\circ  - \widehat {DEC}\)    (2)

Từ (1) và (2) suy ra: \(\widehat {DCA} = \widehat {DEB}.\)

Xét \(\Delta ACD\) và \(\Delta BED\) có:

\(DC = DE\,\, (gt)\)

\(\widehat {DCA} = \widehat {DEB}\left( {cmt} \right)\)

\(\widehat {{D_2}} = \widehat {{D_1}}\,\,(gt)\)

\( \Rightarrow \Delta ACD = \Delta BED\,\,(g.c.g)\)

\( \Rightarrow AD = BD\) (hai cạnh tương ứng).

Xét hai tam giác vuông \(DCF\) và \(DEG\) có:

 \(\widehat {CFD} = \widehat {EGD} = 90^\circ \)

\(DC = DE\,(gt)\)

\(\widehat {{D_2}} = \widehat {{D_1}}\,\left( {cmt} \right)\)

\( \Rightarrow \Delta DCF = \Delta DEG\) (cạnh huyền – góc nhọn).

Ta có: \(\widehat {{D_1}} = \widehat {{D_2}}\,\,(gt)\)

\( \Rightarrow \widehat {{D_1}} + \widehat {CDE} = \widehat {{D_2}} + \widehat {CDE}\)

\( \Rightarrow \widehat {BDC} = \widehat {ADE}\)

Xét \(\Delta ADE\) và \(\Delta BDC\) có:

\(DE = DC\,\,(gt)\)

\(\widehat {ADE} = \widehat {BDC}\,\,(cmt)\)

\(\widehat {AED} = \widehat {BCD}\) (vì \(\Delta CDE\) cân tại \(D\))

\( \Rightarrow \Delta ADE = \Delta BDC\,\,(g.c.g)\)

Do đó đáp án D sai.