Câu hỏi:
2 năm trước
Cho tam giác \(DEF\) và tam giác \(HKI\) có: \(\widehat D = \widehat H = 90^\circ \), \(\widehat F = \widehat I\), \(DF = HI.\) Biết \(\widehat F = {55^0}\). Số đo góc \(K\) là:
Trả lời bởi giáo viên
Đáp án đúng: b
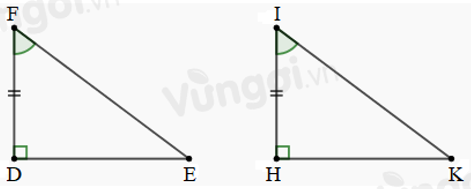
Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta DEF\), ta có:
\(\widehat D + \widehat E + \widehat F = {180^o}\)
\( \Rightarrow \widehat E = {180^o} - \left( {\widehat D + \widehat F} \right)\)
\( \Rightarrow \widehat E = {180^o} - \left( {{{90}^o} + {{55}^o}} \right) = {35^o}\)
Xét hai tam giác vuông \(DEF\) và \(HKI\) có:
\(\begin{array}{l}\widehat D = \widehat H = {90^0}\\\widehat F = \widehat I\;\;\left( {gt} \right)\\DF = HI\;\;\left( {gt} \right)\end{array}\)
\( \Rightarrow \Delta DEF = \Delta HKI\) (cạnh góc vuông - góc nhọn kề).
\( \Rightarrow \widehat E = \widehat K = 35^\circ \) (hai góc tương ứng).
Hướng dẫn giải:
- Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta DEF\) từ đó tính số đo \(\widehat E.\)
- Sử dụng trường hợp bằng nhau cạnh góc vuông-góc nhọn kề của tam giác vuông để chứng minh \(\Delta DEF = \Delta HKI\), từ đó suy ra \(\widehat E = \widehat K\) (hai góc tương ứng bằng nhau), từ đó tìm được số đo \(\widehat K.\)
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
