Cho tam giác ABC có: \(\widehat B + \widehat C = \widehat A\) và \(\widehat C = 2\widehat B\). Tia phân giác của góc $C$ cắt $AB$ tại $D$. Tính \(\widehat {ADC}\) và \(\widehat {BDC}\).

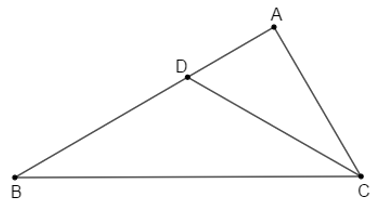
Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta ABC\), ta có:

\(\widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat B + \widehat C + \widehat B + \widehat C = {180^o}\)  (vì \(\widehat B + \widehat C = \widehat A\))

\( \Rightarrow 2\left( {\widehat B + \widehat C} \right) = {180^o}\)

\( \Rightarrow \widehat B + \widehat C = {180^o}:2 = {90^o}\)

Mặt khác \(\widehat C = 2\widehat B\,\,(gt)\) nên \(\widehat B + 2\widehat B = {90^o} \Rightarrow 3\widehat B = {90^o} \Rightarrow \widehat B = {90^o}:3 = {30^o}\).

\( \Rightarrow \widehat C = {90^o} - {30^o} = {60^o}\)

Vì \(CD\) là phân giác của \(\widehat {ACB}\) nên \(\widehat {ACD} = \widehat {BCD} = \dfrac{{\widehat {ACB}}}{2} = \dfrac{{{{60}^o}}}{2} = {30^o}.\)

\(\widehat {ADC}\) là góc ngoài tại đỉnh \(D\) của \(\Delta BCD\) nên ta có:

\(\widehat {ADC} = \widehat B + \widehat {BCD} = {30^o} + {30^o} = {60^o}.\)

\(\widehat {ADC}\) và \(\widehat {BDC}\) là hai góc kề bù nên \(\widehat {ADC} + \widehat {BDC} = {180^o}\)

\( \Rightarrow \widehat {BDC} = {180^o} - \widehat {ADC} = {180^o} - {60^o} = {120^o}.\)