Trả lời bởi giáo viên
Đáp án đúng: d
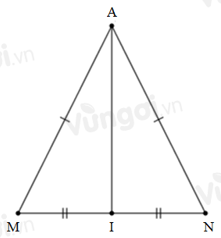
Xét ΔAIM và ΔAIN có:
AM=AN(gt)
IM=IN (vì I là trung điểm của MN)
AI cạnh chung
⇒ΔAIM=ΔAIN(c−c−c)
⇒^AIM=^AIN và ^AMI=^ANI (hai góc tương ứng bằng nhau)
Mặt khác ^AIM+^AIN=180∘ (hai góc kề bù)
⇒^AIM=^AIN=180∘2=90∘. Hay AI⊥MN.
Vậy A, B, C đều đúng.
Hướng dẫn giải:
Chứng minh ΔAIM=ΔAIN từ đó suy ra các cặp góc tương ứng bằng nhau.
* Chú ý: Tổng số đo hai góc kề bù bằng 180o.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
