Trả lời bởi giáo viên
Đáp án đúng: a
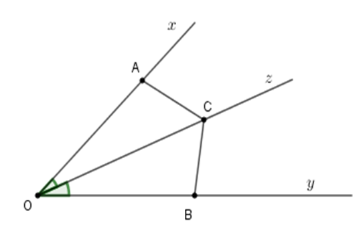
Xét tam giác \(AOC\) và \(BOC\) có
+ \(OA = OB\left( {gt} \right)\)
+ \(\widehat {AOC} = \widehat {BOC}\) (tính chất tia phân giác)
+ Cạnh $OC$ chung
Suy ra \(\Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow AC = BC\) (hai cạnh tương ứng); \(\widehat {OAC} = \widehat {OBC}\); \(\widehat {OCA} = \widehat {OCB}\) (hai góc tương ứng)
Từ đó \(CO\) là tia phân giác của \(\widehat {BCA}.\)
Nên B, C, D đúng, A sai.
Hướng dẫn giải:
Chứng minh hai tam giác bằng nhau theo trường hợp thứ hai và tính chất hai tam giác bằng nhau.

