Câu hỏi:
2 năm trước
Cho tam giác \(ABC,\) kẻ \(BD\) vuông góc với \(AC,\) kẻ \(CE\) vuông góc với \(AB.\) Trên tia đối của tia \(BD\) lấy điểm \(H\) sao cho \(BH = AC.\) Trên tia đối của tia \(CE,\) lấy điểm \(K\) sao cho \(CK = AB.\) So sánh \(AH,AK.\)
Trả lời bởi giáo viên
Đáp án đúng: c
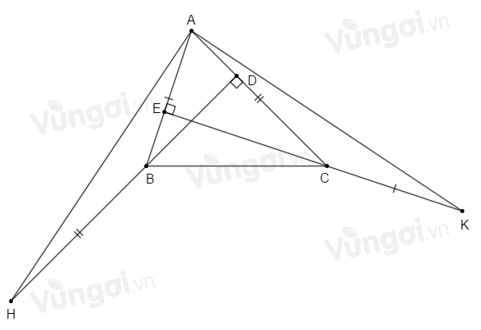
Ta có \(\widehat {ABH}\) là góc ngoài đỉnh \(B\) của \(\Delta ABD\) nên \(\widehat {ABH} = \widehat {BAD} + \widehat {ADB} = \widehat {BAD} + {90^o}\) (1)
\(\widehat {KCA}\) là góc ngoài đỉnh \(C\) của \(\Delta ACE\) nên \(\widehat {KCA} = \widehat {EAC} + \widehat {AEC} = \widehat {EAC} + {90^o}\) (2)
Từ (1) và (2) suy ra \(\widehat {ABH} = \widehat {KCA}\).
Xét \(\Delta ABH\) và \(\Delta KCA\) có:
\(AB = KC\,(gt)\)
\(BH = CA\,(gt)\)
\(\widehat {ABH} = \widehat {KCA}\) (chứng minh trên)
\( \Rightarrow \Delta ABH = \Delta KCA\,(c.g.c)\)
\( \Rightarrow AH = AK\) (hai cạnh tương ứng bằng nhau).
Hướng dẫn giải:
- Sử dụng tính chất góc ngoài tam giác để chứng minh \(\widehat {ABH} = \widehat {KCA}\).
- Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh \(\Delta ABH = \Delta KCA\), từ đó suy ra hai cạnh tương ứng bằng nhau.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
