Trả lời bởi giáo viên
Đáp án đúng: a
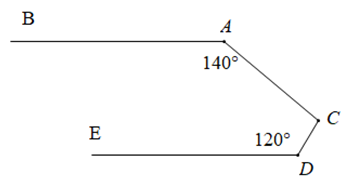
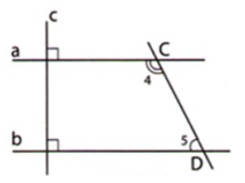
Trong \(\widehat {ACD}\) vẽ tia \(CF\) song song với \(AB\).
Vì \(AB//\,CF\) (theo cách vẽ) nên \(\widehat {BAC} + \widehat {{C_1}} = {180^o}\) (2 góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {{C_1}} = {180^o} - \widehat {BAC} = {180^o} - {140^o} = {40^o}.\)
Theo đề bài ta có: \(AB//DE\) và \(CF//AB\) (theo cách vẽ) nên \(CF//DE\)
Vì \(CF//DE\) nên \(\widehat {{C_2}} + \widehat {CDE} = {180^o}\) (2 góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {{C_2}} = {180^o} - \widehat {CDE} = {180^o} - {120^o} = {60^o}.\)
Vì tia \(CF\) nằm trong \(\widehat {ACD}\) nên tia \(CF\) nằm giữa hai tia \(CA\) và tia \(CD\), ta có:
\(\widehat {ACD} = \widehat {{C_1}} + \widehat {{C_2}} = {40^o} + {60^o} = {100^o}.\)
Hướng dẫn giải:
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
+ Áp dụng tính chất hai đường thẳng song song.
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
