Vẽ \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\). Sau đó vẽ tiếp \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
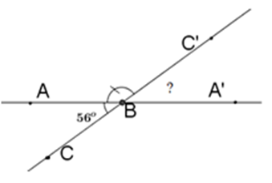
Vì góc \(ABC'\) kề bù với góc $ABC$ nên $BC'$ là tia đối của tia $BC.$
Vì góc $C'BA'$ kề bù với góc $ABC'$ nên $BA'$ là tia đối của tia $BA.$
Do đó, góc $C'BA'$ và góc $ABC$ đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).
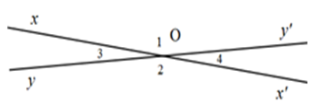
\({\widehat O_2} = {\widehat O_1} = {165^o}\) (tính chất hai góc đối đỉnh)
Góc ${O_1}$ và góc ${O_4}$ là hai góc kề bù
\( \Rightarrow {\widehat O_1} + {\widehat O_4} = {180^o}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {\widehat O_1}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {165^o} = {15^o}\)
\({\widehat O_3} = {\widehat O_4} = {15^o}\,\) (hai góc đối đỉnh)
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
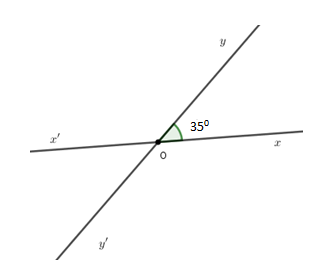
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 35^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 35^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 35^\circ \)
\( \Rightarrow \widehat {x'Oy} = 145^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 145^\circ .\)
Hai góc có số đo bằng ${145^o}$ là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Hai đường thẳng $xy$ và $x'y'$ cắt nhau tại $O.$ Biết \(\widehat {xOx'} = {70^o}\). $Ot$ là tia phân giác của góc xOx’. $Ot'$ là tia đối của tia $Ot.$ Tính số đo góc $yOt'.$
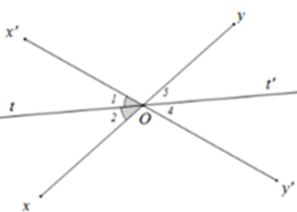
Vì $Ot$ là tia phân giác của góc $xOx'$ nên
\(\widehat {xOt} = \widehat {tOx'} = \dfrac{1}{2}\widehat {xOx'} = \dfrac{1}{2}{.70^o} = {35^o}\)
Vì $Oy$ là tia đối của $Ox,Ot'$ là tia đối của $Ot$
\( \Rightarrow \widehat {yOt'} = \widehat {xOt} = {35^o}\) (tính chất hai góc đối đỉnh).
Hai đường thẳng $MN$ và $PQ$ cắt nhau tại $O$, tạo thành góc $MOP$ có số đo bằng ${80^o}.$
Chọn câu đúng.
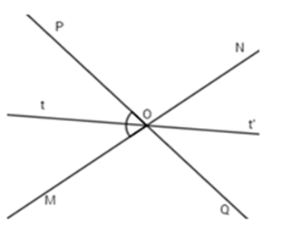
$\widehat {NOQ} = \widehat {MOP} = {80^o}$ (tính chất hai góc đối đỉnh)
Vì góc $MOP$ và $PON$ là hai góc kề bù nên :
$\,\widehat {MOP} + \widehat {PON} = {180^o} \Rightarrow {80^o} + \widehat {PON} = {180^o}$ $ \Rightarrow \widehat {PON} = {180^o} - {80^o} = {100^o}$
Khi đó $\widehat {MOQ} = \widehat {PON} = {100^o}$ (tính chất hai góc đối đỉnh).
Hai đường thẳng $MN$ và $PQ$ cắt nhau tại $O$, tạo thành góc $MOP$ có số đo bằng ${80^o}.$
Vẽ tia $Ot$ là tia phân giác của góc $MOP,$ $Ot'$ là tia đối của tia $Ot.$ Chọn câu đúng.
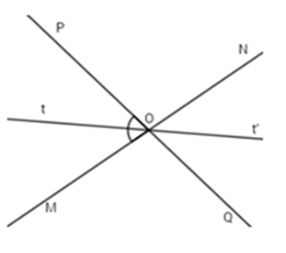
Vì $Ot$ là tia phân giác của góc $MOP$ nên $\widehat {MOt} = \widehat {tOP} = \dfrac{1}{2}\widehat {MOP} = \dfrac{1}{2}{.80^o} = {40^o}.$
Vì $Ot'$ là tia đối của tia $Ot,$ do đó :
\(\widehat {NOt'} = \widehat {MOt} = {40^o}\,\,\,\) (hai góc đối đỉnh)
\(\widehat {t'OQ} = \widehat {tOP} = {40^o}\,\,\,\,\) (hai góc đối đỉnh)
\( \Rightarrow \widehat {NOt'} = \widehat {t'OQ}\)
Mặt khác tia $Ot'$ nằm trong góc $NOQ.$ Vậy $Ot'$ là tia phân giác của góc $NOQ.$
Cho đường thẳng $AB$ và điểm $O$ trên đường thẳng đó. Trên cùng một nửa mặt phẳng bờ $AB$ vẽ hai tia $OC$ và $OD$ sao cho \(\widehat {AOC} = \widehat {BOD} = {50^o}\). Trên nửa mặt phẳng bờ $AB$ không chứa tia $OD,$ vẽ tia $OE$ sao cho tia $OA$ là tia phân giác của góc $COE.$ Chọn câu đúng?
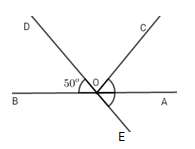
+ Hai góc $AOC$ và $BOD$ có: $OA$ và $OB$ là hai tia đối nhau, $OD$ và $OC$ không phải là hai tia đối nhau.
Vậy hai góc đó không phải là hai góc đối đỉnh.
+ Vì góc $BOD$ và $DOA$ là hai góc kề bù nên:
$\begin{array}{l}\,\,\,\,\,\widehat {BOD} + \widehat {DOA} = {180^O}\\ \Rightarrow {50^O} + \widehat {DOA} = {180^O}\\ \Rightarrow \widehat {DOA} = {180^O} - {50^O} = {130^O}\end{array}$
Tia $OA$ là tia phân giác góc $COE$ nên \(\widehat {AOE} = \widehat {AOC} = {50^O}\).
Tia $OD$ và tia $OE$ thuộc hai nửa mặt phẳng đối nhau bờ chứa tia $OA$ nên tia $OA$ nằm giữa hai tia $OD$ và $OE,$ ta có:
\(\widehat {DOA} + \widehat {AOE} = {130^0} + {50^0} = {180^0}\)
Suy ra $OD$ và $OE$ là hai tia đối nhau.
Hai góc $BOD$ và $AOE$ có hai cặp cạnh $OB$ và $OA,OD$ và $OE$ là hai tia đối nhau nên là hai góc đối đỉnh.
Cho \(\widehat {AOB} = 50^\circ \) , tia \(OC\) là tia phân giác của \(\widehat {AOB}\). Gọi \(OD\) là tia đối của tia \(OC\). Trên nửa mặt phẳng bờ \(CD\) chứa tia \(OA\), vẽ tia \(OE\) sao cho \(\widehat {DOE} = 25^\circ \). Góc nào dưới đây đối đỉnh với \(\widehat {DOE}\).
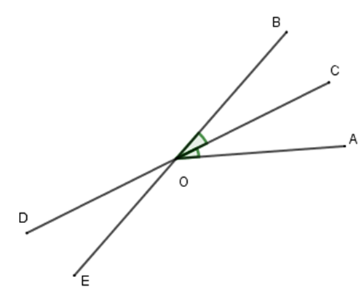
Vì \(OC\) và \(OD\) là hai tia đối nhau nên \(\widehat {COE}\) và \(\widehat {DOE}\) là hai góc kề bù. Khi đó \(\widehat {COE} + \widehat {DOE} = 180^\circ \)\( \Rightarrow \widehat {COE} = 180^\circ - 25^\circ = 155^\circ \)
Vì \(OC\) là tia phân giác của góc \(BOA\) nên \(\widehat {COB} = \dfrac{{\widehat {AOB}}}{2} = \dfrac{{50^\circ }}{2} = 25^\circ \)
Nhận thấy \(\widehat {BOC} + \widehat {COE} = 25^\circ + 155^\circ = 180^\circ \) nên \(OB\) và \(OE\) là hai tia đối nhau.
Suy ra \(\widehat {BOC}\) và \(\widehat {DOE}\) là hai góc đối đỉnh.
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
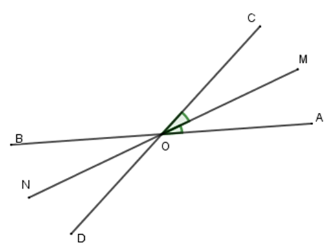
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \dfrac{{\widehat {COA}}}{2} = \dfrac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
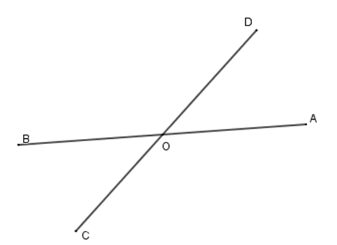
Vì \(\widehat {AOD}\) và \(\widehat {AOC}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {AOC} = 180^\circ \) mà \(\widehat {AOC} - \widehat {AOD} = 50^\circ \)
Nên \(\widehat {AOC} = \dfrac{{180^\circ + 50^\circ }}{2} = 115^\circ \) và \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 65^\circ \)
Mà \(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh nên \(\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Lại có \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh nên \(\widehat {BOD} = \widehat {AOC} = 115^\circ .\)
Vậy \(\widehat {BOD} = \widehat {AOC} = 115^\circ ;\,\widehat {BOC} = \widehat {AOD} = 65^\circ .\)

