Câu hỏi:
2 năm trước
Cho \(\widehat {AOB} = 60^\circ \), tia \(OC\) là tia phân giác của \(\widehat {AOB}\). Gọi \(OD\) là tia đối của tia \(OA\). Trên nửa mặt phẳng bờ \(AD\) không chứa tia \(OB\), vẽ tia \(OI\) sao cho \(\widehat {DOI} = 30^\circ \). Góc nào dưới đây đối đỉnh với \(\widehat {AOC}\).
Trả lời bởi giáo viên
Đáp án đúng: d
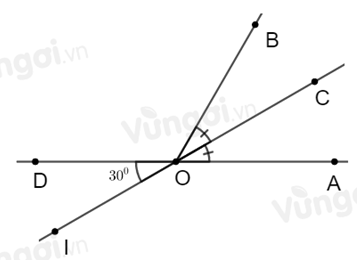
Vì tia \(OD\) là tia đối của tia \(OA\) nên \(\widehat {DOI}\) và \(\widehat {AOI}\) là hai góc kề bù.
Khi đó \(\widehat {DOI} + \widehat {AOI} = 180^\circ \) \( \Rightarrow \widehat {AOI} = {180^0} - \widehat {DOI}\) \( \Rightarrow \widehat {AOI} = {180^0} - {30^0} = {150^0}\)
Vì \(OC\) là tia phân giác của \(\widehat {AOB}\) nên \(\widehat {AOC} = \dfrac{{\widehat {AOB}}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\)
Xét hai góc kề \(\widehat {AOI}\) và \(\widehat {AOC}\) ta có: \(\widehat {AOI} + \widehat {AOC} = {150^0} + {30^0} = {180^0}\) suy ra \(\widehat {AOI}\) và \(\widehat {AOC}\) là hai góc kề bù.
Do đó tia \(OI\) là tia đối của tia \(OC\).
Mặt khác tia \(OD\) là tia đối của tia \(OA\) nên \(\widehat {DOI}\) và \(\widehat {AOC}\) là hai góc đối đỉnh.
Hướng dẫn giải:
+ Tính \(\widehat {AOI}\) bằng cách sử dụng: “Hai góc kề bù có tổng bằng \({180^0}\)”
+ Tính \(\widehat {AOC}\) bằng cách sử dụng tính chất tia phân giác của một góc: “Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat {xOz} = \widehat {yOz} = \dfrac{{\widehat {xOy}}}{2}\).”
+ Chứng minh tia \(OI\) là tia đối của tia \(OC\).
+ Từ đó suy ra góc đối đỉnh với \(\widehat {AOC}\) theo định nghĩa: “Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia”.
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
