Câu hỏi:
2 năm trước
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) tạo thành \(\widehat {AOC} = 100^\circ \). Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
Trả lời bởi giáo viên
Đáp án đúng: b
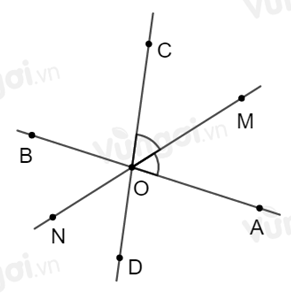
Vì \(OM\) là tia phân giác \(\widehat {AOC}\) nên \(\widehat {AOM} = \widehat {COM} = \dfrac{{\widehat {AOC}}}{2} = \dfrac{{{{100}^0}}}{2} = {50^0}\)
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OB\) là tia đối của tia \(OA\), \(OD\) là tia đối của tia \(OC\)
Mặt khác \(ON\) là tia đối của tia \(OM\) nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh.
Suy ra \(\widehat {BON} = \widehat {AOM} = {50^0};\widehat {DON} = \widehat {COM} = {50^0}\) hay \(\widehat {BON} = \widehat {DON} = {50^0}.\)
Hướng dẫn giải:
+ Tính các góc \(\widehat {AOM};\widehat {COM}\) bằng cách sử dụng tính chất tia phân giác của một góc: “Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat {xOz} = \widehat {yOz} = \dfrac{{\widehat {xOy}}}{2}\).”
+ Xác định góc đối đỉnh với \(\widehat {BON}\) và góc đối đỉnh với \(\widehat {DON}\) theo định nghĩa: “Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia”
+ Tính \(\widehat {BON}\) và \(\widehat {DON}\) bằng cách sử dụng tính chất hai góc đối đỉnh: “Hai góc đối đỉnh thì bằng nhau.”
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
