Câu hỏi:
2 năm trước
Trên đường thẳng \(AA'\) lấy điểm \(O.\) Vẽ trên cùng nửa mặt phẳng bờ \(AA'\) tia \(OB\) và tia \(OD\) sao cho \(\widehat {AOB} = \widehat {A'OD} = {45^o}.\) Tính góc \(BOD.\)
Trả lời bởi giáo viên
Đáp án đúng: d
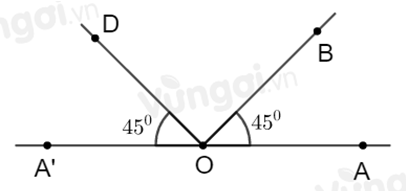
Vì \(\widehat {AOD}\) và \(\widehat {DOA'}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {DOA'} = {180^0}\)
\( \Rightarrow \widehat {AOD} = {180^0} - \widehat {DOA'}\)
\( \Rightarrow \widehat {AOD} = {180^0} - {45^0} = {135^0}\)
Ta có: tia \(OB\) và tia \(OD\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(OA\) và \(\widehat {AOB} < \widehat {AOD}\,(do\,{45^o} < {135^o})\) nên tia \(OB\) nằm giữa hai tia \(OA\) và \(OD\).
Do đó \(\widehat {AOB} + \widehat {BOD} = \widehat {AOD}\) \( \Rightarrow {45^0} + \widehat {BOD} = {135^0}\) \( \Rightarrow \widehat {BOD} = {135^0} - {45^0} = {90^0}\).
Hướng dẫn giải:
+ Sử dụng: “Hai góc kề bù có tổng bằng \({180^0}\)” để tính góc \(AOD.\)
+ Sử dụng dấu hiệu nhận biết tia nằm giữa hai tia: “Nếu các tia \(Oy\) và \(Oz\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\) và \(\widehat {xOy} < \widehat {xOz}\) thì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\)” để chứng minh tia \(OB\) nằm giữa hai tia \(OA\) và \(OD\), từ đó tính góc \(BOD.\)
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
