Trả lời bởi giáo viên
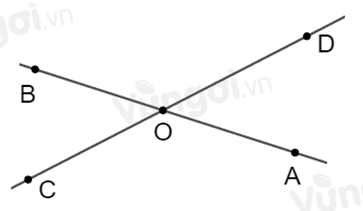
Vì ^AOD và ^AOC là hai góc kề bù nên ^AOD+^AOC=180∘ mà ^AOC=3^AOD
⇒^AOD+3^AOD=180∘ ⇒4^AOD=180∘ ⇒^AOD=180∘:4=45∘
Do đó ^AOC=3^AOD=3.450=1350
Vì hai đường thẳng AB và CD cắt nhau tại O nên hai tia OB và OA là hai tia đối nhau, hai tia OD và OC là hai tia đối nhau.
Do đó ^BOD và ^AOC là hai góc đối đỉnh; ^AOD và ^BOC là hai góc đối đỉnh
Kh đó ^BOD=^AOC=135∘;^BOC=^AOD=45∘
Vậy ^BOD=^AOC=135∘; ^BOC=^AOD=45∘.
Hướng dẫn giải:
+ Tính ^AOD và ^AOC bằng cách sử dụng : “Hai góc kề bù có tổng bằng 1800” và ^AOC=3^AOD.
+ Xác định góc đối đỉnh với ^BOD và góc đối đỉnh với ^BOC theo định nghĩa: “Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia”
+ Tính ^BOD và ^BOC bằng cách sử dụng tính chất hai góc đối đỉnh: “Hai góc đối đỉnh thì bằng nhau.”