Đề thi khảo sát chất lượng đầu năm - Đề số 1

Sử dụng kết quả câu trên ngày thứ ba bạn Mai đọc được $96$ trang.

Số trang bạn Mai đọc trong ngày thứ ba chiếm số phần trăm tổng số trang của cuốn sách là:

$\dfrac{{96}}{{240}}.100\%  = 40\%$

+) Đường tròn $\left( {0;8cm} \right)$ là đường tròn có bán kính bằng $8cm$, đường kính bằng $8.2 = 16cm$ $\Rightarrow$ Khẳng định (1) sai.

+) Tam giác $HKM$ là hình tạo bởi $3$ đoạn thẳng $HK,KM,MH$ khi ba điểm $H,K,M$ không thẳng hàng $\Rightarrow$ Khẳng định (2) đúng.

+) $ƯCLN\left( {14,19} \right) = 1$ nên $\dfrac{{14}}{{19}}$ là phân số tối giản $\Rightarrow$ Khẳng định (3) đúng.

+) Chiều dài của mảnh vườn là $36cm,$ trên bản đồ là $0,36m$ thì tỉ lệ xích của bản đồ là $\dfrac{{0,36}}{{36}} = \dfrac{1}{{100}}$ $\Rightarrow$ Khẳng định (4) sai.

+) $1,5.5,1 = 7,65 \ne 1$ $\Rightarrow$ Khẳng định (5) sai.

Vậy có ba khẳng định sai.

$\begin{array}{l}10 - |x - 1| = \dfrac{{ - 20}}{7}.\dfrac{7}{{ - 5}}\\10 - |x - 1| = 4\\|x - 1| = 10 - 4\\|x - 1| = 6\end{array}$

+) TH1: $x - 1 = 6$

              $x = 6 + 1$

              $x = 7$

+) TH2: $x - 1 =  - 6$

              $x =  - 6 + 1$

              $x =  - 5$

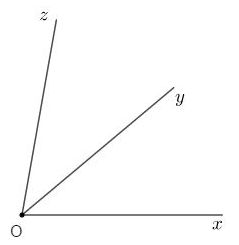
Vì trên cùng một nửa mặt phẳng có bờ chứa tia $Ox$, $\widehat {xOy} < \widehat {xOz}\,\left( {{{40}^o} < {{80}^o}} \right)$ nên tia $Oy$ nằm giữa hai tia $Ox,\,Oz$.

Ta có: $\widehat {xOy} + \widehat {yOz} = \widehat {xOz}$

$\Rightarrow \widehat {yOz} = \widehat {xOz} - \widehat {xOy} = {80^o} - {40^o} = {40^o}.$

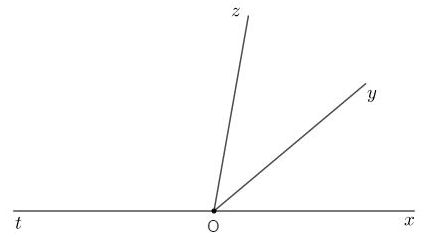
$Ot$ là tia đối của tia $Ox$ nên $\widehat {xOy}$ và $\widehat {yOt}$ là hai góc kề bù nên ta có:

$\widehat {xOy} + \widehat {yOt} = {180^o}$

$\Rightarrow \widehat {yOt} = {180^o} - \widehat {xOy}$$\, = {180^o} - {40^o} = {140^o}$

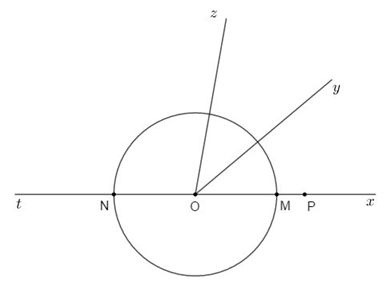
TH1:

$\left( {O;3cm} \right)$ cắt $Ox$ tại $M$và cắt $Ot$ tại $N$.

Ta có $P$ nằm trên $Ox$, $N$ nằm trên $Ot$ mà $Ox$ và $Ot$ là hai tia đối nhau nên $O$ nằm giữa hai điểm $N$ và $P.$

Ta có: $NP = NO + OP = 3 + 4 = 7\left( {cm} \right).$

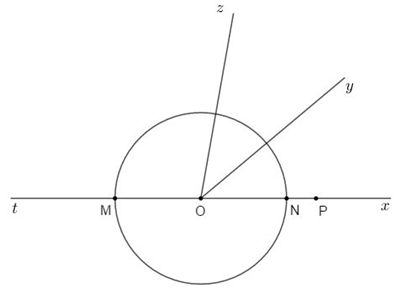
TH2:

$\left( {O;3cm} \right)$ cắt $Ox$ tại $N$ và cắt $Ot$ tại $M.$

Trên tia $Ox$ ta có $ON < OP\,\left( {3cm < 4cm} \right)$ nên $N$ nằm giữa $O$ và $P.$

Ta có: $ON + NP = OP$

$\Rightarrow NP = OP - ON = 4 - 3 = 1\left( {cm} \right).$

Ta có:

$\begin{array}{l}7M = \dfrac{{7.\left( {{7^{2013}} + 1} \right)}}{{{7^{2014}} + 1}} = \dfrac{{{{7.7}^{2013}} + 7.1}}{{{7^{2014}} + 1}}\\ \,\,\,\,\,\,\,\,\,= \dfrac{{{7^{2014}} + 7}}{{{7^{2014}} + 1}} = \dfrac{{{7^{2014}} + 1 + 6}}{{{7^{2014}} + 1}} \\\,\,\,\,\,\,\,\,\,= \dfrac{{{7^{2014}} + 1}}{{{7^{2014}} + 1}} + \dfrac{6}{{{7^{2014}} + 1}} \\\,\,\,\,\,\,\,\,\,= 1 + \dfrac{6}{{{7^{2014}} + 1}}\end{array}$

$\begin{array}{l}7N = \dfrac{{7.\left( {{7^{2014}} + 1} \right)}}{{{7^{2015}} + 1}} = \dfrac{{{{7.7}^{2014}} + 7.1}}{{{7^{2015}} + 1}}\\\,\,\,\,\,\,\,\,\, = \dfrac{{{7^{2015}} + 7}}{{{7^{2015}} + 1}}= \dfrac{{{7^{2015}} + 1 + 6}}{{{7^{2015}} + 1}}\\\,\,\,\,\,\,\,\,\, = \dfrac{{{7^{2015}} + 1}}{{{7^{2015}} + 1}} + \dfrac{6}{{{7^{2015}} + 1}}\\\,\,\,\,\,\,\,\,\, = 1 + \dfrac{6}{{{7^{2015}} + 1}}\end{array}$

Vì ${7^{2015}} + 1 > {7^{2014}} + 1$  nên $\dfrac{6}{{{7^{2014}} + 1}} > \dfrac{6}{{{7^{2015}} + 1}}$

Do đó $7M > 7N$ hay $M > N.$