Câu hỏi:
2 năm trước
Trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\) vẽ hai tia \(Oy\) và \(Oz\) sao cho \(\widehat {xOy} = {40^0},\widehat {xOz} = {80^0}\).
Vẽ tia \(Ot\) là tia đối của tia \(Ox\), đường tròn tâm \(O\) bán kính \(3cm\) cắt đường thẳng \(xt\) tại hai điểm \(M,N\). Trên tia \(Ox\) lấy điểm \(P\) sao cho \(OP = 4cm\) . Độ dài đoạn thẳng \(NP\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
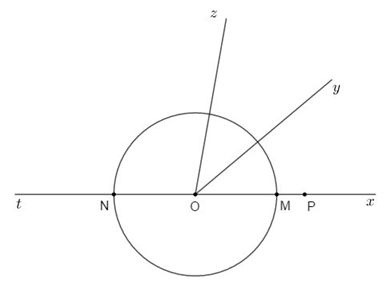
TH1:
\(\left( {O;3cm} \right)\) cắt \(Ox\) tại \(M\)và cắt \(Ot\) tại \(N\).
Ta có \(P\) nằm trên \(Ox\), \(N\) nằm trên \(Ot\) mà \(Ox\) và \(Ot\) là hai tia đối nhau nên \(O\) nằm giữa hai điểm \(N\) và \(P.\)
Ta có: \(NP = NO + OP = 3 + 4 = 7\left( {cm} \right).\)
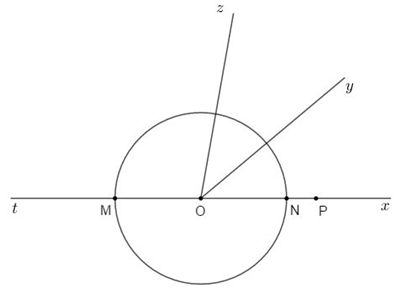
TH2:
\(\left( {O;3cm} \right)\) cắt \(Ox\) tại \(N\) và cắt \(Ot\) tại \(M.\)
Trên tia \(Ox\) ta có \(ON < OP\,\left( {3cm < 4cm} \right)\) nên \(N\) nằm giữa \(O\) và \(P.\)
Ta có: \(ON + NP = OP\)
\( \Rightarrow NP = OP - ON = 4 - 3 = 1\left( {cm} \right).\)
Hướng dẫn giải:
Xét hai trường hợp:
TH1: \(N\) thuộc tia \(Ot.\)
TH2: \(N\) thuộc tia \(Ox.\)
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - đề số 1 toán 7 có lời giải
- Đề thi khảo sát chất lượng đầu năm - đề số 4 toán 7 có lời giải
- Đề thi khảo sát chất lượng đầu năm - đề số 2 toán 7 có lời giải
- Đề thi khảo sát chất lượng đầu năm - đề số 3 toán 7 có lời giải
- Đề thi khảo sát chất lượng đầu năm - đề số 5 toán 7 có lời giải
