Câu hỏi:
2 năm trước
Trên cùng một nửa mặt phẳng bờ chứa tia \(Om\), vẽ hai tia \(On\) và \(Ot\) sao cho \(\widehat {mOn} = {120^o},\,\widehat {mOt} = {60^o}.\)
Số đo \(\widehat {nOt}\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
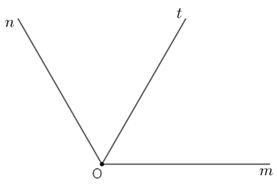
Trên cùng một nửa mặt phẳng bờ chứa tia \(Om\) có \(\widehat {mOn} > \,\widehat {mOt}\left( {{{120}^o} > {{60}^o}} \right)\) nên tia \(Ot\) nằm giữa hai tia \(Om,\,On.\)
Ta có: \(\widehat {mOt} + \widehat {nOt} = \widehat {mOn}\)
\(\begin{array}{l} \Rightarrow \widehat {nOt} = \widehat {mOn} - \widehat {mOt}\\ \Rightarrow \widehat {nOt} = {120^o} - {60^o} = {60^o}\end{array}\)
Hướng dẫn giải:
Chứng minh tia \(Ot\) nằm giữa hai tia \(Om,\,On.\)
Ta có: \(\widehat {mOt} + \widehat {nOt} = \widehat {mOn}\)
Từ đó ta tìm được số đo \(\widehat {nOt}\)
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - đề số 1 toán 7 có lời giải
- Đề thi khảo sát chất lượng đầu năm - đề số 4 toán 7 có lời giải
- Đề thi khảo sát chất lượng đầu năm - đề số 2 toán 7 có lời giải
- Đề thi khảo sát chất lượng đầu năm - đề số 3 toán 7 có lời giải
- Đề thi khảo sát chất lượng đầu năm - đề số 5 toán 7 có lời giải
