Trên cùng một nửa mặt phẳng bờ chứa tia \(Om\), vẽ hai tia \(On\) và \(Ot\) sao cho \(\widehat {mOn} = {120^o},\,\widehat {mOt} = {60^o}.\)
Gọi tia \(Ox\) là tia đối của tia \(Om\). Số đo \(\widehat {xOn}\) là:
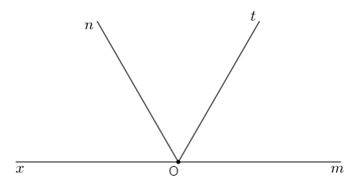
Vì \(Ox\) là tia đối của tia \(Om\) nên \(\widehat {xOn}\) và \(\widehat {mOn}\) là hai góc kề bù, do đó ta có:
\(\widehat {xOn} + \widehat {mOn} = {180^o}\)
\(\Rightarrow \widehat {xOn} = {180^o} - \widehat {mOn} \)\(\,= {180^o} - {120^o} = {60^o}\)
Cho \(A = \left( {\dfrac{1}{{{2^2}}} - 1} \right).\left( {\dfrac{1}{{{3^2}}} - 1} \right).\left( {\dfrac{1}{{{4^2}}} - 1} \right)...\left( {\dfrac{1}{{{{100}^2}}} - 1} \right)\)
Giá trị của biểu thức A là:
Ta có A là tích của \(99\) số âm , nên \(A < 0\) . Do đó:
\(A = -\left( {1 - \dfrac{1}{{{2^2}}}} \right).\left( {1 - \dfrac{1}{{{3^2}}}} \right).\left( {1 - \dfrac{1}{{{4^2}}}} \right)\)\(\,...\left( {1 - \dfrac{1}{{{{100}^2}}}} \right)\)
\(A = - \left( {1 - \dfrac{1}{4}} \right).\left( {1 - \dfrac{1}{9}} \right).\left( {1 - \dfrac{1}{{16}}} \right)\)\(\,...\left( {1 - \dfrac{1}{{10000}}} \right)\)
\(A = - \left( {\dfrac{3}{{{2^2}}}} \right..\dfrac{8}{{{3^2}}}.\dfrac{{15}}{{{4^2}}}...\left. {\dfrac{{9999}}{{{{100}^2}}}} \right)\)
\(A = - \left( {\dfrac{{1.3}}{{{2^2}}}} \right..\dfrac{{2.4}}{{{3^2}}}.\dfrac{{3.5}}{{{4^2}}}...\left. {\dfrac{{99.101}}{{{{100}^2}}}} \right)\)
\(A = - \left( {\dfrac{{1.2.3...98.99}}{{2.3.4...99.100}}} \right..\left. {\dfrac{{3.4.5...100.101}}{{2.3.4...99.100}}} \right)\)
\(A = - \left( {\dfrac{1}{{100}}} \right..\left. {\dfrac{{101}}{2}} \right) = - \dfrac{{101}}{{200}}\)

