Trả lời bởi giáo viên
Đáp án đúng: b
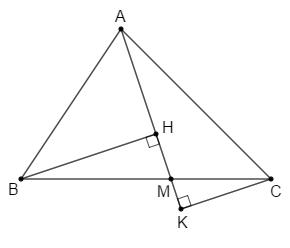
Kẻ BH⊥AM;CK⊥AM (H,K∈AM).
Theo đề bài ta có d=BH+CK
+ Trường hợp 1: Nếu AM không vuông góc với BC khi đó:
BH,BM lần lượt là đường vuông góc và đường xiên kẻ từ B đến AM suy ra BM>BH (1)
CK,CM lần lượt là đường vuông góc và đường xiên kẻ từ C đến AM suy ra CM>CK (2)
Cộng (1) với (2) theo vế với vế ta được:
BM+CM>BH+CK hay BC>d.
+ Trường hợp 2: Nếu AM⊥BCkhi đó H,M,K trùng nhau.
Tam giác ABC có hai góc B,C nhọn nên M nằm giữa hai điểm B và C do đó BH+CK=BM+CM hay BC=d.
Vậy d≤BC.
Hướng dẫn giải:
Kẻ BH⊥AM;CK⊥AM (H,K∈AM).
Theo đề bài ta có d=BH+CK
+ Trường hợp 1: Nếu AM không vuông góc với BC
So sánh BM>BH; CM>CK từ đó so sánh BC với d.
+ Trường hợp 2: Nếu AM⊥BC khi đó H,M,K trùng nhau từ đó so sánh BC với d.


