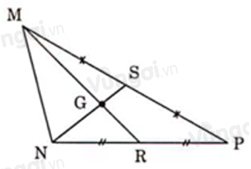
Cho tam giác \(ABC\) có các đường trung tuyến \(BD\) và \(CE\) vuông góc với nhau. Tính độ dài cạnh \(BC\) biết \(BD = 4,5\,cm;\,CE = 6\,cm.\)

\(BC = 6\,cm.\)

\(BC = 4\,,5cm.\)

\(BC = 5\,cm.\)

\(BC = 10\,cm.\)

Xem đáp án

60 lượt xem

Tính chất ba đường trung tuyến của tam giác - MÔN TOÁN - Lớp 7. Thi ngay

Trả lời bởi giáo viên

Đáp án đúng: c

Gọi giao điểm của hai đường trung tuyến \(BD\) và \(CE\) là \(G\) thì \(G\) là trọng tâm tam giác \(ABC.\)

Theo tính chất ba đường trung tuyến của tam giác ta có: \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\)

Mà \(BD = 4,5\,cm;\,CE = 6\,cm\) nên \(BG = \dfrac{2}{3}.4,5 = 3\,cm;\,CG = \dfrac{2}{3}.6\, = 4\,cm.\)

Xét tam giác \(BGC\) vuông tại G (do \(BD\) và \(CE\) vuông góc với nhau tại G), theo định lý Py-ta-go ta có:

\(B{C^2} = B{G^2} + C{G^2}\)

\(B{C^2} = {3^2} + {4^2} = 25\) hay \(BC = 5\,cm.\)

Vậy \(BC = 5\,cm.\)

Hướng dẫn giải:

+ Sử dụng định lý về tính chất ba đường trung tuyến của một tam giác để tính \(BG;CG\): Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó. Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.

+ Sử dụng định lý Py-ta-go để tính cạnh \(BC:\) Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.