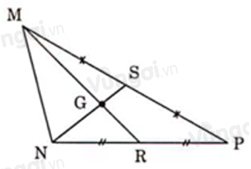
Cho tam giác \(MNP,\) hai đường trung tuyến \(ME\) và \(NF\) cắt nhau tại \(O.\) Tính diện tích tam giác \(MNP,\) biết diện tích tam giác \(MNO\) là \(12c{m^2}\).

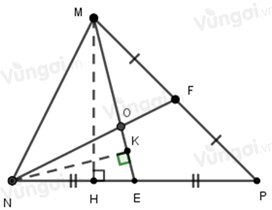
Gọi \(MH\) là đường cao kẻ từ \(M\) xuống cạnh \(NP;NK\) là đường cao kẻ từ \(N\) xuống cạnh \(ME.\)

Hai đường trung tuyến \(ME\) và \(NF\) cắt nhau tại \(O\)  nên \(O\) là trọng tâm tam giác \(MNP,\) do đó \(MO = \dfrac{2}{3}ME\).

Có \(ME\) là đường trung tuyến ứng với cạnh \(NP\) nên \(E\)  là trung điểm của \(NP,\) suy ra: \(NP = 2.NE\)

Ta có:

\(\dfrac{{{S_{MNO}}}}{{{S_{MNE}}}} = \dfrac{{\dfrac{1}{2}.NK.MO}}{{\dfrac{1}{2}.NK.ME}} = \dfrac{{\dfrac{1}{2}.NK.\dfrac{2}{3}.ME}}{{\dfrac{1}{2}.NK.ME}} = \dfrac{2}{3}\,\,\,\,\,\,\,\,\, \Rightarrow {S_{MNE}} = \dfrac{3}{2}{S_{MNO}}\)

\(\dfrac{{{S_{MNE}}}}{{{S_{MNP}}}} = \dfrac{{\dfrac{1}{2}.MH.NE}}{{\dfrac{1}{2}.MH.NP}} = \dfrac{{\dfrac{1}{2}.MH.NE}}{{\dfrac{1}{2}.MH.2.NE}} = \dfrac{1}{2}\,\,\,\,\,\,\,\,\, \Rightarrow {S_{MNP}} = 2{S_{MNE}}\)

Từ đó suy ra:

\({S_{MNP}} = 2.{S_{MNE}} = 2.\dfrac{3}{2}.{S_{MNO}} = 3.{S_{MNO}} \Rightarrow {S_{MNP}} = 3.12 = 36\,c{m^2}\).