Trả lời bởi giáo viên
Đáp án đúng: a
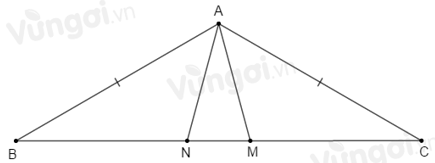
\(\Delta ABC\) cân ở \(A\) nên \(\widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A}}{2} = \dfrac{{{{180}^o} - {{120}^o}}}{2} = {30^0}\).
Xét \(\Delta AMB\) có: BM = BA(gt) nên \(\Delta AMB\) cân ở \(B.\)
Do đó \(\widehat {AMB} = \dfrac{{{{180}^0} - \widehat B}}{2} = \dfrac{{{{180}^0} - {{30}^0}}}{2} = {75^o}\)
Xét \(\Delta ANC\) có: \(CN = CA\) (vì cùng bằng \(AB\)) nên \(\Delta ANC\) cân ở \(C\).
Do đó \(\widehat {ANC} = \dfrac{{{{180}^0} - \widehat C}}{2} = \dfrac{{{{180}^0} - {{30}^0}}}{2} = {75^o}\).
Xét \(\Delta AMN\) có: \(\widehat {AMN} = \widehat {ANM} = {75^o}\), do đó \(\Delta AMN\) cân ở \(A.\)
Hướng dẫn giải:
Để chứng minh tam giác \(AMN\) cân, ta chứng minh hai góc ở đáy bằng nhau \(\widehat {AMN} = \widehat {ANM}\).
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
