Cho tam giác \(ABC\) cân tại đỉnh \(A\) với \(\widehat A < {90^0}\). Kẻ \(BD \bot AC\) tại \(D.\) Trên cạnh \(AB,\) lấy điểm \(E\) sao cho \(AE = AD.\) Chọn câu sai.

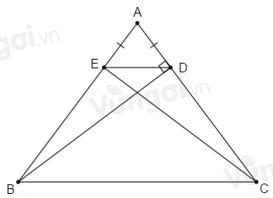
Do tam giác ABC cân tại \(A\) nên \(\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2}\)            (1)

Ta thấy \(\Delta ADE\) có: \(AD = AE\,\,(gt)\) nên \(\Delta ADE\) cân tại \(A\).

\( \Rightarrow \widehat {AED} = \dfrac{{{{180}^0} - \widehat A}}{2}\)                     (2)

Từ (1) và (2) suy ra: \(\widehat B = \widehat {AED}\). Mặt khác hai góc này ở vị trí đồng vị nên \(DE//BC.\)

Vậy A đúng.

Xét \(\Delta ABD\) và \(\Delta ACE\) có:

\(\widehat A\) chung

\(AD = AE\,(gt)\)

\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))

\( \Rightarrow \Delta ABD = \Delta ACE\,(c.g.c)\)

\( \Rightarrow \widehat {ADB} = \widehat {AEC} = {90^o}\) (hai góc tương ứng).

Do đó \(\Delta ACE\) là tam giác vuông.