Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM > \dfrac{{BC}}{2}\). Chọn câu đúng.

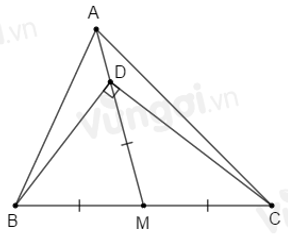
Trên tia \(MA\) lấy điểm \(D\) sao cho: \(MD = \dfrac{{BC}}{2}\), khi đó \(D\) nằm giữa \(A\) và \(M.\)

Ta có: \(\widehat {BDM}\) là góc ngoài đỉnh \(D\) của \(\Delta ABD\) nên \(\widehat {BDM} = \widehat {BAD} + \widehat {ABD}\) suy ra \(\widehat {BDM} > \widehat {BAD}\)   (1)

          \(\widehat {CDM}\) là góc ngoài đỉnh \(D\) của \(\Delta ACD\) nên \(\widehat {CDM} = \widehat {CAD} + \widehat {ACD}\) suy ra \(\widehat {CDM} > \widehat {CAD}\)   (2)

\(\Delta BMD\) có: \(MB = MD\)(theo cách dựng) nên \(\Delta BMD\) cân tại \(M\), suy ra \(\widehat {MBD} = \widehat {BDM}\)

\(\Delta CMD\) có: \(MC = MD\) (theo cách dựng) nên \(\Delta CMD\) cân tại \(M\), suy ra \(\widehat {MCD} = \widehat {CDM}\)

Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta BDC\), ta có:

\(\widehat {CBD} + \widehat {BDC} + \widehat {BCD} = {180^o}\)

\( \Rightarrow \widehat {CBD} + \widehat {BDM} + \widehat {CDM} + \widehat {BCD} = {180^o}\)

\( \Rightarrow 2\widehat {BDM} + 2\widehat {CDM} = {180^o}\)

\( \Rightarrow 2\left( {\widehat {BDM} + \widehat {CDM}} \right) = {180^o}\)

\( \Rightarrow 2\widehat {BDC} = {180^o}\)

\( \Rightarrow \widehat {BDC} = \dfrac{{{{180}^o}}}{2} = {90^o}\)                    (3)

Từ (1), (2) và (3) ta có:

\(\widehat {BAD} + \widehat {CAD} < \widehat {BDM} + \widehat {CDM}\)

\( \Rightarrow \widehat {BAC} < \widehat {BDC}\)

\( \Rightarrow \widehat {BAC} < {90^o}\).