Tam giác \(ABC\) có \(\widehat A = 45^\circ ;\,\widehat B - \widehat C = 35^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)

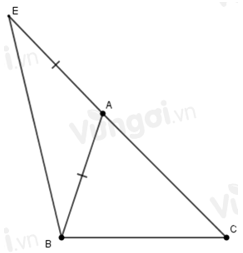
Xét tam giác \(ABC\) có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)  (định lí tổng ba góc của tam giác) và \(\widehat A = 45^\circ ;\,\widehat B - \widehat C = 35^\circ \,\left( {gt} \right)\)

Suy ra \(\widehat B + \widehat C = {180^o} - \widehat A = {180^o} - {45^o} = 135^\circ \)

Suy ra \(\widehat B = \dfrac{{135^\circ  + 35^\circ }}{2} = 85^\circ ;\,\widehat C = {135^o} - {85^o} = 50^\circ \)

Xét tam giác \(AEB\) cân tại \(A\) (do \(AB = AE\,\left( {gt} \right)\)) nên \(\widehat {AEB} = \widehat {ABE}\) (tính chất tam giác cân) (1)

Lại có: \(\widehat {BAC}\) là góc ngoài tại đỉnh \(A\)của tam giác \(AEB \Rightarrow \widehat {BAC} = \widehat {AEB} + \widehat {ABE}\)  (2)

Từ (1) và (2) suy ra: \(\widehat {ABE} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{45}^o}}}{2} = {22^o}30'\)

Do đó \(\widehat {CBE} = \widehat {CBA} + \widehat {ABE} = 85^\circ  + 22^\circ 30' = 107^\circ 30'.\)