Trả lời bởi giáo viên
Đáp án đúng: c
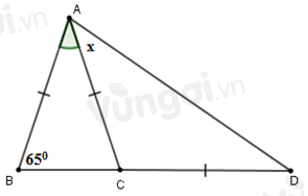
Tam giác \(ABC\) cân tại \(A\) (vì \(AB = AC\) ) nên \(\widehat B = \widehat {ACB} = {65^o}\).
\(\widehat {ACB} + \widehat {ACD} = {180^o}\) (hai góc kề bù)
\( \Rightarrow \widehat {ACD} = {180^o} - \widehat {ACB} = {180^o} - {65^o} = {115^o}.\)
Tam giác \(ACD\) cân tại \(C\) (vì \(CA = CD\)) và \(\widehat {ACD} = {115^o}\) nên \(\widehat {CAD} = \dfrac{{{{180}^o} - \widehat {ACD}}}{2} = \dfrac{{{{180}^o} - {{115}^o}}}{2} = {32^o}30'\)
Vậy \(x = {32^o}30'.\)
Hướng dẫn giải:
Sử dụng tính chất tổng ba góc của một tam giác, tính chất góc ngoài và sử dụng tính chất của tam giác cân.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
