Trong hình vẽ dưới đây có:

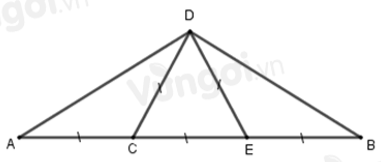
Từ hình vẽ ta có: \(DC = CE = ED = EB = CA\).

Vì \(DC = CE = ED\) nên \(\Delta CDE\) là tam giác đều.

Vì \(DC = CA\) nên \(\Delta ACD\) cân tại \(C.\)

Vì \(ED = EB\) nên \(\Delta BED\) cân tại \(E.\)

\(\Delta CDE\) là tam giác đều nên \(\widehat {DCE} = \widehat {DEC} = {60^o}\).

Ta có: \(CA = EB\)

\( \Rightarrow CA + CE = EB + CE\)

\( \Rightarrow AE = BC\)

Xét \(\Delta ADE\) và \(\Delta BDC\) có:

\(DE = DC\,(gt)\)

\(AE = BC\,(cmt)\)

\(\widehat {DEA} = \widehat {DCB} = {60^o}\)

\( \Rightarrow \Delta ADE = \Delta BDC\,(c.g.c)\)

\( \Rightarrow DA = DB\) (hai cạnh tương ứng).

\(\Delta ADB\) có \(DA = DB\) (cmt) nên \(\Delta ADB\) cân tại \(D\).

Vậy hình vẽ có 1 tam giác đều và 3 tam giác cân.