Cho tam giác $ABC$ vuông tại $A$ có $BD$ là phân giác góc $ABC$ ($D \in AC$), kẻ $DE$ vuông góc với $BC$ ($E$ thuộc $BC$ ). Trên tia đối của tia $AB$ lấy điểm $F$ sao cho $AF = CE.$ Chọn câu đúng.
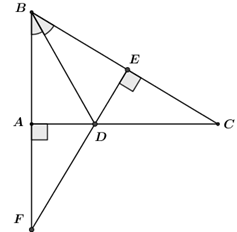
+) $DE$ vuông góc với $BC$ nên ta có tam giác $BDE$ là tam giác vuông.
Xét hai tam giác vuông $BAD$ và $BED$ ta có:
\(\widehat {ABD} = \widehat {EBD}\) (do $BD$ là tia phân giác của góc $B$ )
$BD$ là cạnh chung
Vậy \(\Delta BAD = \Delta BED\) (cạnh huyền – góc nhọn).
\( \Rightarrow \left\{ \begin{array}{l}AB = BE\\AD = DE\end{array} \right.\) (các cặp cạnh tương ứng).
\( \Rightarrow B;\;D\) nằm trên đường trung trực của $AE$ hay $BD$ là đường trung trực của $AE.$ Do đó A đúng.
+) Xét hai tam giác vuông $ADF$ và $EDC$ ta có:
$AF{\rm{ }} = {\rm{ }}EC$ (gt)
$DA = DE$ (cmt)
Vậy \(\Delta ADF = \Delta EDC\) (hai cạnh góc vuông bằng nhau).
Suy ra $DF = DC$ (hai cạnh tương ứng). Do đó B đúng.
+) Trong tam giác vuông $ADF,{\rm{ }}AD$ là cạnh góc vuông, $DF$ là cạnh huyền nên \(DA < DF.\)
Mà $DF = DC$ (cmt). Từ đó suy ra \(AD < DC.\) Do đó C đúng.
Vậy cả A, B, C đều đúng.
Cho tam giác $ABC$ cân tại $A,$ vẽ trung tuyến $AM.$ Từ $M$ kẻ $ME$ vuông góc với $AB$ tại $E,$ kẻ $MF$ vuông góc với $AC$ tại $F.$ Từ $B$ kẻ đường thẳng vuông góc với $AB$ tại $B$, từ $C$ kẻ đường thẳng vuông góc với $AC$ tại $C$, hai đường thẳng này cắt nhau tại $D$. Chọn câu sai.
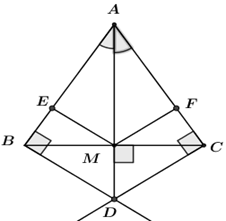
+) Tam giác $ABC$ cân tại $A$ có $AM$ là đường trung tuyến nên $AM$ đồng thời là tia phân giác của góc $A$.
Ta có $ME$ vuông góc với $AB$ tại $E$ nên $AEM$ là tam giác vuông tại $E$; $MF$ vuông góc với $AC$ tại $F$ nên $AFM$ là tam giác vuông tại $F$
Xét hai tam giác vuông $AEM$ và $AFM$ ta có
$AM$ là cạnh chung
\(\widehat {EAM} = \widehat {FAM}\) (do $AM$ là tia phân giác của góc $A$)
Vậy \(\Delta AEM = \Delta {\rm{AF}}M\) (cạnh huyền – góc nhọn)
+ ) Vì \(\Delta AEM = \Delta {\rm{AF}}M\)suy ra :
\(AE = AF\) (hai cạnh tương ứng bằng nhau)
\(ME = MF\) (hai cạnh tương ứng bằng nhau)
Do đó hai điểm $A$, $M$ nằm trên đường trung trực của $EF$.
Vậy $AM$ là đường trung trực của $EF$.
+) Xét hai tam giác vuông: \(\Delta ABD\) vuông tại B, \(\Delta ACD\) vuông tại $C$ ta có:
\(AB = AC\) (do tam giác $ABC$ cân tại $A$)
$AD$ là cạnh chung
Vậy \(\Delta ABD = \Delta ACD\) (cạnh huyền – cạnh góc vuông)
Suy ra \(DB = DC\) (hai cạnh tương ứng bằng nhau)
Do đó $D$ thuộc tia phân giác của góc $A$ (1) (vì điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó).
Lại có $AM$ là tia phân giác của góc $A$, hay $M$ thuộc tia phân giác của góc $A$ (2)
Từ (1) và (2) suy ra 3 điểm $A,{\rm{ }}M,{\rm{ }}D$ thẳng hàng.
Ta chưa đủ điều kiện để chỉ ra được \(M\) là trung điểm của \(AD.\)
Cho tam giác $ABC$ vuông tại $A$, góc $B$ bằng \({60^o}\). Vẽ $AH$ vuông góc với $BC$ tại $H$. Lấy điểm $D$ thuộc tia đối của tia $HA$ sao cho $HD = HA.$
So sánh $AB$ và $AC,$ $BH$ và $HC$
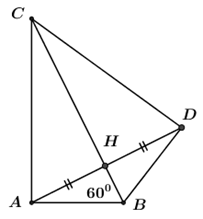
+) Tam giác $ABC$ vuông tại $A$ nên ta có:
\(\widehat B + \widehat C = {90^o} \Rightarrow \widehat C = {90^o} - \widehat B = {90^o} - {60^o} = {30^o}\)
Trong tam giác ABC ta có \(\widehat B > \widehat C\) suy ra $AC > AB.$
Xét tam giác $ABC$ vuông tại $A$ có:
$BH$ là hình chiếu của $AB$ trên $BC$; $HC$ là hình chiếu của $AC$ trên $BC$
Mà \(AB < AC\) (cmt)
Suy ra \(BH < HC.\)
Cho tam giác $ABC$ vuông tại $A$, góc $B$ bằng \({60^o}\). Vẽ $AH$ vuông góc với $BC$ tại $H$. Lấy điểm $D$ thuộc tia đối của tia $HA$ sao cho $HD = HA.$
Tính số đo của góc $BDC.$

+ Ta có $AH$ vuông góc với $BC$ tại $H$ và điểm $D$ thuộc tia đối của tia $HA$ nên tam giác $AHC$ vuông tại $A$, tam giác $DHC$ vuông tại $H.$
Xét hai tam giác vuông $AHC$ và $DHC$ ta có:
$AH = HD$ (gt)
$HC$ là cạnh chung
Vậy $\Delta AHC{\rm{ = }}\Delta DHC$ (hai cạnh góc vuông)
+) Ta có $\Delta AHC{\rm{ = }}\Delta DHC \Rightarrow \widehat {ACH} = \widehat {DCH} = {30^o}$(2 góc tương ứng) và $AC = DC$ (2 cạnh tương ứng)
Xét hai tam giác $ABC$ và $DBC$ ta có:
$BC$ là cạnh chung
$AC = CD$
$\widehat {ACB} = \widehat {DCB} = {30^o}$
Vậy $\Delta ABC{\rm{ = }}\Delta DBC\,(c.g.c) \Rightarrow \widehat {BAC} = \widehat {BDC} = {90^o}$(2 góc tương ứng)
Vậy \(\widehat {BDC} = {90^o}\)
Cho tam giác $ABC$. Gọi $O$ là giao điểm các đường phân giác của tam giác đó. Từ $O$ kẻ $OD$, $OE$, $OF$ lần lượt vuông góc với $BC, AC, AB.$ Trên tia đối của các tia $AC, BA, CB$ lấy theo thứ tự ba điểm \({A_1};{B_1};{C_1}\) sao cho \(A{A_1} = BC;\,B{B_1} = AC;\,C{C_1} = AB\)
Chọn câu đúng.
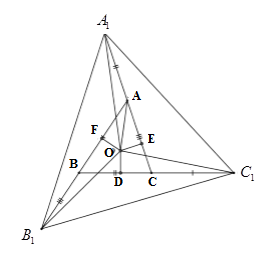
+ Do $OD, OE, OF$ lần lượt vuông góc với $BC, AC, AB$ nên các tam giác $AOE, AOF, BOF, BOD, COE, COD$ là các tam giác vuông.
$O$ là giao điểm các đường phân giác nên suy ra $OD = OE = OF.$
Xét hai tam giác vuông $AOE$ và $AOF$ ta có:
$AO$ là cạnh chung;
$OE = OF$
Vậy $\Delta AOE{\rm{ = }}\Delta AOF$ (cạnh huyền – cạnh góc vuông)
Suy ra $AE =AF$ (2 cạnh tương ứng)
Chứng minh tương tự ta có: $BD = BF, CD = CE.$
Cho tam giác $ABC$. Gọi $O$ là giao điểm các đường phân giác của tam giác đó. Từ $O$ kẻ $OD$, $OE$, $OF$ lần lượt vuông góc với $BC, AC, AB.$ Trên tia đối của các tia $AC, BA, CB$ lấy theo thứ tự ba điểm \({A_1};{B_1};{C_1}\) sao cho \(A{A_1} = BC;\,B{B_1} = AC;\,C{C_1} = AB\)
Chọn câu đúng.
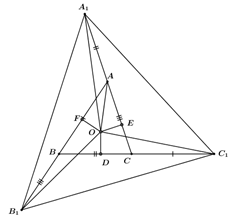
+ Đặt $BC = a,{\rm{ }}CA = b,{\rm{ }}AB = c$ . Ta có:
$\begin{array}{*{20}{l}}{AE = AC-CE = AC-CD}\\{AF = AB-BF = AB-BD}\end{array}$
Suy ra $AE + AF = AC-CD + AB-BD = AB + AC-\left( {BD + CD} \right)$
Hay $2.AE = AB + AC-\;BC = c + b-a.$
Do đó \(AE = \dfrac{{c + b - a}}{2}\)
Ta có \(E{A_1} = EA + {\rm{A}}{{\rm{A}}_1} = EA + BC = \dfrac{{c + b - a}}{2} + a = \dfrac{{c + b + a}}{2}\)
Chứng minh tương tự ta có: \(F{B_1} = \dfrac{{c + b + a}}{2};\,\,D{C_1} = \dfrac{{c + b + a}}{2}\)
Vậy \(E{A_1} = F{B_1} = D{C_1}.\)

