Cho tam giác $ABC$ cân tại $A,$ vẽ trung tuyến $AM.$ Từ $M$ kẻ $ME$ vuông góc với $AB$ tại $E,$ kẻ $MF$ vuông góc với $AC$ tại $F.$  Từ $B$ kẻ đường thẳng vuông góc với $AB$ tại $B$, từ $C$ kẻ đường thẳng vuông góc với $AC$ tại $C$, hai đường thẳng này cắt nhau tại $D$. Chọn câu sai.

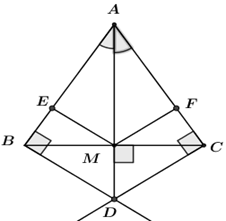
+) Tam giác $ABC$ cân tại $A$ có $AM$ là đường trung tuyến nên $AM$ đồng thời là tia phân giác của góc $A$.

Ta có $ME$ vuông góc với $AB$ tại $E$ nên $AEM$ là tam giác vuông tại $E$; $MF$ vuông góc với $AC$ tại $F$ nên $AFM$ là tam giác vuông tại $F$

Xét hai tam giác vuông $AEM$ và $AFM$ ta có

$AM$ là cạnh chung

\(\widehat {EAM} = \widehat {FAM}\) (do $AM$ là tia phân giác của góc $A$)

Vậy \(\Delta AEM = \Delta {\rm{AF}}M\) (cạnh huyền – góc nhọn)

+ ) Vì \(\Delta AEM = \Delta {\rm{AF}}M\)suy ra :

\(AE = AF\) (hai cạnh tương ứng bằng nhau)

\(ME = MF\) (hai cạnh tương ứng bằng nhau)

Do đó hai điểm $A$, $M$ nằm trên đường trung trực của $EF$.

Vậy $AM$ là đường trung trực của $EF$.

+) Xét hai tam giác vuông: \(\Delta ABD\) vuông tại B, \(\Delta ACD\)  vuông tại $C$ ta có:

\(AB = AC\) (do tam giác $ABC$ cân tại $A$)

$AD$ là cạnh chung

Vậy \(\Delta ABD = \Delta ACD\) (cạnh huyền – cạnh góc vuông)

Suy ra \(DB = DC\) (hai cạnh tương ứng bằng nhau)

Do đó $D$ thuộc tia phân giác của góc $A$ (1) (vì điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó).

Lại có $AM$ là tia phân giác của góc $A$, hay $M$ thuộc tia phân giác của góc $A$ (2)

Từ (1) và (2) suy ra 3 điểm  $A,{\rm{ }}M,{\rm{ }}D$ thẳng hàng.

Ta chưa đủ điều kiện để chỉ ra được \(M\) là trung điểm của \(AD.\)