Trả lời bởi giáo viên
Đáp án đúng: a
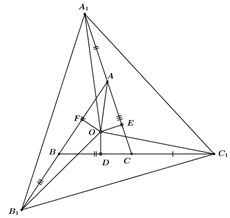
+ Do $OD, OE, OF$ lần lượt vuông góc với $BC, AC, AB$ nên các tam giác $AOE, AOF, BOF, BOD, COE, COD$ là các tam giác vuông.
$O$ là giao điểm các đường phân giác nên suy ra $OD = OE = OF.$
Xét hai tam giác vuông $AOE$ và $AOF$ ta có:
$AO$ là cạnh chung;
$OE = OF$
Vậy $\Delta AOE{\rm{ = }}\Delta AOF$(cạnh huyền – cạnh góc vuông)
Suy ra $AE =AF$ (2 cạnh tương ứng)
Chứng minh tương tự ta có: $BD = BF, CD = CE.$
Hướng dẫn giải:
Áp dụng tính chất hai tam giác bằng nhau.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
