Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$ có $BD$ là phân giác góc $ABC$ ($D \in AC$), kẻ $DE$ vuông góc với $BC$ ($E$ thuộc $BC$ ). Trên tia đối của tia $AB$ lấy điểm $F$ sao cho $AF = CE.$ Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: d
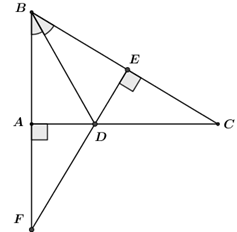
+) $DE$ vuông góc với $BC$ nên ta có tam giác $BDE$ là tam giác vuông.
Xét hai tam giác vuông $BAD$ và $BED$ ta có:
\(\widehat {ABD} = \widehat {EBD}\) (do $BD$ là tia phân giác của góc $B$ )
$BD$ là cạnh chung
Vậy \(\Delta BAD = \Delta BED\) (cạnh huyền – góc nhọn).
\( \Rightarrow \left\{ \begin{array}{l}AB = BE\\AD = DE\end{array} \right.\) (các cặp cạnh tương ứng).
\( \Rightarrow B;\;D\) nằm trên đường trung trực của $AE$ hay $BD$ là đường trung trực của $AE.$ Do đó A đúng.
+) Xét hai tam giác vuông $ADF$ và $EDC$ ta có:
$AF{\rm{ }} = {\rm{ }}EC$ (gt)
$DA = DE$ (cmt)
Vậy \(\Delta ADF = \Delta EDC\) (hai cạnh góc vuông bằng nhau).
Suy ra $DF = DC$ (hai cạnh tương ứng). Do đó B đúng.
+) Trong tam giác vuông $ADF,{\rm{ }}AD$ là cạnh góc vuông, $DF$ là cạnh huyền nên \(DA < DF.\)
Mà $DF = DC$ (cmt). Từ đó suy ra \(AD < DC.\) Do đó C đúng.
Vậy cả A, B, C đều đúng.
Hướng dẫn giải:
+) Áp dụng tính chất hai tam giác bằng nhau, tính chất tia phân giác.
+) Áp dụng mối quan hệ giữa đường vuông góc và đường xiên.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
