Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$, góc $B$ bằng \({60^o}\). Vẽ $AH$ vuông góc với $BC$ tại $H$. Lấy điểm $D$ thuộc tia đối của tia $HA$ sao cho $HD = HA.$
So sánh $AB$ và $AC,$ $BH$ và $HC$
Trả lời bởi giáo viên
Đáp án đúng: a
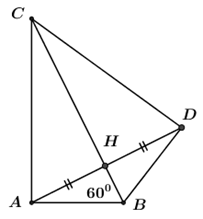
+) Tam giác $ABC$ vuông tại $A$ nên ta có:
\(\widehat B + \widehat C = {90^o} \Rightarrow \widehat C = {90^o} - \widehat B = {90^o} - {60^o} = {30^o}\)
Trong tam giác ABC ta có \(\widehat B > \widehat C\) suy ra $AC > AB.$
Xét tam giác $ABC$ vuông tại $A$ có:
$BH$ là hình chiếu của $AB$ trên $BC$; $HC$ là hình chiếu của $AC$ trên $BC$
Mà \(AB < AC\) (cmt)
Suy ra \(BH < HC.\)
Hướng dẫn giải:
+) Áp dụng mối quan hệ giữa cạnh và góc trong tam giác, giữa đường vuông góc và đường xiên.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
