Câu hỏi:
2 năm trước
Cho ΔMNP có: ˆM=900, các tia phân giác của ˆN và ˆP cắt nhau tại I. Gọi D,E là chân các đường vuông góc hạ từ I đến các cạnh MN và MP. Tính IE biết ID=4cm.
Trả lời bởi giáo viên
Đáp án đúng: d
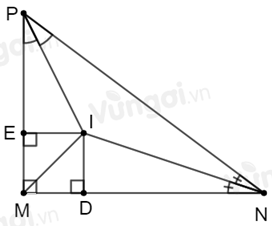
Xét ΔMNP có các tia phân giác của ^MNP và ^MPN cắt nhau tại I nên I là giao điểm của ba đường phân giác trong ΔMNP.
Khi đó ID=IE (tính chất ba đường phân giác của tam giác) mà ID=4cm suy ra IE=4cm.
Hướng dẫn giải:
Sử dụng định lí về tính chất ba đường phân giác của tam giác: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.

