Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ \). Các đường phân giác $AD$ và \(BE.\) Tính số đo góc \(BED.\)
Trả lời bởi giáo viên
Đáp án đúng: d
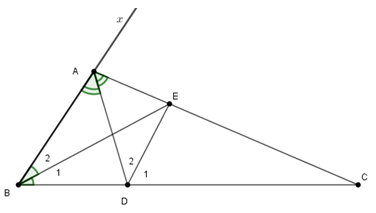
Gọi \(Ax\) là tia đối của tia \(AB.\) Ta có \(\widehat {BAD} = \widehat {DAC} = 60^\circ \) nên \(\widehat {CAx} = 60^\circ .\)
Xét \(\Delta ABD\) có \(AE\) là tia phân giác của góc ngoài đỉnh \(A,\)\(BE\) là tia phân giác của góc \(B\) và chúng cắt nhau tại \(E\) nên \(DE\) là phân giác góc ngoài của góc \(D.\)
Mà \(\widehat {EDC}\) là góc ngoài tại đỉnh \(D\) của tam giác \(BED\) nên \(\widehat {{B_1}} + \widehat {BED} = \widehat {EDC}\)
Do đó \(\widehat {BED} = \widehat {{D_1}} - \widehat {{B_1}} = \dfrac{{\widehat {ADC} - \widehat {ABC}}}{2} = \dfrac{{\widehat {BAD}}}{2} = 30^\circ \)
Hướng dẫn giải:
Áp dụng định lý về góc ngoài của một tam giác, tính chất tia phân giác của một góc.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
