Cho tam giác \(ABC\) có phân giác \(AD\) thỏa mãn \(BD = 2DC.\) Trên tia đối tia \(CB\) lấy điểm \(E\) sao cho \(BC = CE.\) Khi đó tam giác \(ADE\) là tam giác:

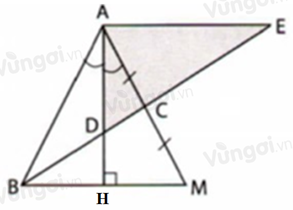
Kéo dài \(AC\) lấy điểm \(M\) sao cho: \(CM = AC\), kéo dài \(AD\) cắt \(BM\) tại \(H\)

Vì \(AD\) là phân giác của \(\widehat {BAM}\) nên \(\widehat {BAH} = \widehat {HAM} = \dfrac{{\widehat {BAM}}}{2}\) (tính chất tia phân giác)

Xét \(\Delta ABM\) có: \(BC\) là đường trung tuyến ứng với cạnh \(AM\), \(BD = 2DC\) (gt)

Do đó \(D\) là trọng tâm của \(\Delta ABM\)

Suy ra \(AD\) là đường trung tuyến của \(\Delta ABM\)

Xét \(\Delta ABM\) có: \(AD\) là đường trung tuyến đồng thời là đường phân giác

Do đó \(\Delta ABM\) cân tại \(A\) \( \Rightarrow \widehat {ABM} = \widehat {AMB}\) (tính chất tam giác cân)

Trong \(\Delta ABM\) có: \(\widehat {BAM} + \widehat {ABM} + \widehat {AMB} = {180^0}\) ( định lý tổng ba góc của tam giác)

\( \Rightarrow \widehat {BAM} + 2\widehat {ABM} = {180^0} \Rightarrow \dfrac{{\widehat {BAM}}}{2} + \widehat {ABM} = {90^0}\) hay \(\widehat {BAH} + \widehat {ABH} = {90^0}\)

Xét \(\Delta ABH\) có:

\(\widehat {BAH} + \widehat {ABH} + \widehat {AHB} = {180^0}\) (định lý tổng ba góc của tam giác)

\( \Rightarrow \widehat {AHB} = {180^0} - (\widehat {BAH} + \widehat {ABH}) = {180^0} - {90^0} = {90^0}\)

\( \Rightarrow AH \bot BM\) hay \(AD \bot BM\)

Xét \(\Delta ACE\) và \(\Delta MCB\) có:

\(AC = CM\)

\(BC = CE\,(gt)\)

\(\widehat {ACE} = \widehat {MCB}\) (hai góc đối đỉnh)

\( \Rightarrow \Delta ACE = \Delta MCB\,(c.g.c)\) \( \Rightarrow \widehat {AEC} = \widehat {MBC}\) (hai góc tương ứng)

Mà \(\widehat {AEC};\widehat {MBC}\) ở vị trí so le trong

\( \Rightarrow AE//BM\) (dấu hiệu nhận biết hai đường thẳng song song)

Mà \(AD \bot BM \Rightarrow AD \bot AE\) (quan hệ giữa tính vuông góc với tính song song)

Do đó \(\Delta ADE\) vuông tại \(A\).