Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có \(AB < AC.\) Trên đường phân giác \(AD\) lấy điểm \(E.\) Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
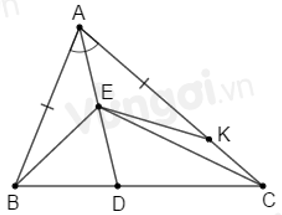
Trên cạnh \(AC\) lấy điểm \(K\) sao cho: \(AK = AB\).
Xét \(\Delta ABE\) và \(\Delta AKE\) có:
\(AB = AK\) (cách dựng)
\(\widehat {BAE} = \widehat {KAE}\) (vì \(AD\) là tia phân giác \(\widehat {BAC}\))
\(AE\) cạnh chung
\( \Rightarrow \Delta ABE = \Delta AKE\,(c.g.c)\)
\( \Rightarrow EB = EK\) (hai cạnh tương ứng).
Áp dụng bất đẳng thức tam giác vào \(\Delta CEK\) ta có: \(EC - EK < KC\) mà \(EK = EB\,\,(cmt)\) suy ra \(EC - EB < KC\) (1)
Mặt khác: \(KC = AC - AK = AC - AB\) (vì \(AK = AB\) theo cách dựng) (2)
Từ (1) và (2) suy ra: \(EC - EB < AC - AB.\)
Hướng dẫn giải:
Trên cạnh \(AC\) lấy điểm \(K\) sao cho: \(AK = AB\). Chứng minh \(\Delta ABE = \Delta AKE\,(c.g.c)\) suy ra \(EB = EK\) (hai cạnh tương ứng).
Áp dụng bất đẳng thức tam giác chứng minh \(EC - EK < KC\) mà \(EK = EB\,\,(cmt)\) suy ra \(EC - EB < KC\)
Mặt khác: \(KC = AC - AK = AC - AB\), từ đó suy ra điều phải chứng minh.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
