Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có điểm \(M\) là một điểm bất kì nằm trong tam giác. So sánh \(MB + MC\) và \(AB + AC\).
Trả lời bởi giáo viên
Đáp án đúng: b
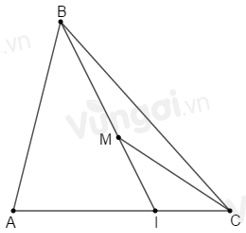
Gọi \(I\) là giao điểm của \(BM\) và \(AC\).
Áp dụng bất đẳng thức tam giác vào \(\Delta IMC\) ta có: \(MC < MI + IC\) (1)
Cộng \(MB\) vào hai vế (1) ta được: \(MC + MB < MI + IC + MB\)
\( \Rightarrow MC + MB < MI + MB + IC\)
\( \Rightarrow MC + MB < IB + IC\) (2)
Áp dụng bất đẳng thức tam giác vào \(\Delta IBA\) ta có: \(IB < IA + AB\) (3)
Cộng \(IC\) vào hai vế (3) ta được: \(IB + IC < IA + AB + IC\)
\( \Rightarrow IB + IC < IA + IC + AB\)
\( \Rightarrow IB + IC < AC + AB\) (4)
Từ (2) và (4) suy ra \(MB + MC < AB + AC\).
Hướng dẫn giải:
Gọi \(I\) là giao điểm của \(BM\) và \(AC\).
Áp dụng bất đẳng thức tam giác chứng minh:
\(MC < MI + IC\)\( \Rightarrow MC + MB < IB + IC\)
\(IB < IA + AB\) \( \Rightarrow IB + IC < AC + AB\)
Từ đó suy ra điều phải chứng minh.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
