Xe có khối lượng m = 800kg đang chuyển động thẳng đều thì hãm phanh chuyển động chậm dần đều. Biết quãng đường đi được trong giây cuối cùng của chuyển động là 1,5m. Hỏi lực hãm của xe nhận giá trị nào trong các giá trị sau?
Quãng đường vật đi trong 1s cuối là: \(\Delta S = {S_t} - {S_{t - 1}}\)
\(\begin{array}{l} \Rightarrow 1,5 = {v_0}t + \dfrac{1}{2}a{t^2} - \left[ {{v_0}\left( {t - 1} \right) + \dfrac{1}{2}a{{\left( {t - 1} \right)}^2}} \right]\\ \Leftrightarrow 1,5 = {v_0}t + \dfrac{1}{2}a{t^2} - {v_0}t + {v_0} - \dfrac{1}{2}a{t^2} + at - \dfrac{1}{2}a\\ \Leftrightarrow 1,5 = {v_0} + at - \dfrac{a}{2}\left( 1 \right)\end{array}\)
mặt khác có: \(a = \dfrac{{v - {v_0}}}{t} = \dfrac{{ - {v_0}}}{t}\left( 2 \right)\)
từ (1) và (2) ta có: \( - at + at - \dfrac{a}{2} = 2 \Rightarrow a = - 3m/s\)
do lực tác dụng là lực hãm nên ngược chiều chuyển động
Áp dụng biểu thức định luật II Newton: \( - {F_h} = ma \Rightarrow {F_h} = 800.3 = 2400N\)
Câu nào đúng?Trong một cơn lốc xốy, một hòn đá bay trúng vào một cửa kính, làm vỡ kính.
Theo định luật III Newton ta có: lực của hòn đá tác dụng vào tấm kính về độ lớn bằng lực của tấm kính tác dụng vào hòn đá.
Số giá trị $m$ nguyên để hàm số \(y = \dfrac{{mx + 2}}{{x + m}}\) nghịch biến trên từng khoảng xác định của nó là
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - m} \right\}\).
Hàm số nghịch biến trên từng khoảng xác định của nó \( \Leftrightarrow y' < 0,\forall x \in D.\)
\( \Leftrightarrow \dfrac{{{m^2} - 2}}{{{{\left( {x + m} \right)}^2}}} < 0,\forall x \in D\)\( \Leftrightarrow {m^2} - 2 < 0 \Leftrightarrow m \in \left( { - \sqrt 2 ;\sqrt 2 } \right) \Rightarrow m \in \left\{ { - 1;0;1} \right\}\).
Khi nhận xét về tương tác giữa hai vật đâu là nhận xét sai?
- Ta có: lực- phản lực có độ lớn bằng nhau, là cặp lực trực đối.
Hai lực trực đối là lực tương tác giữa hai vật, có điểm đặt khác nhau và không cân bằng
- Ta có biểu thức định luật II Newton: \(a = \dfrac{F}{m}\) từ đó thấy a tỉ lệ nghịch với khối lượng m.
Hàm số \(y = \dfrac{{{x^2} - 3x}}{{x + 1}}\) có giá trị cực đại bằng:
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có \(y' = \dfrac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}}\), \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\)
Bảng biến thiên:
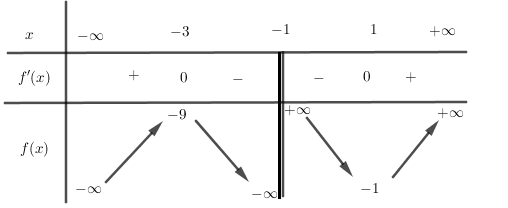
Từ bảng biến thiên ta có hàm số đạt cực đại tại điểm \(x = - 3\), giá trị cực đại là \({y_{CD}} = - 9\)
Hỏi \(a\) và \(b\) thỏa mãn điều kiện nào để hàm số \(y = a{x^4} + b{x^2} + c{\rm{ }}\left( {a \ne 0} \right)\)có đồ thị dạng như hình bên?
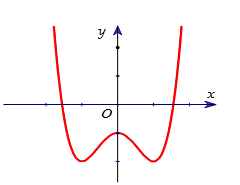
Dựa vào hình dạng của đồ thị ta thấy: hệ số \(a > 0\) và đồ thị có ba cực trị nên \(a\) và $b$ trái dấu.
Vậy \(a > 0\) và \(b < 0\).
Cho hàm số $y = \dfrac{{{m^2}x - 1}}{{x + 1}}$. Kết luận nào sau đây là sai?
Ta có: $y' = \dfrac{{{m^2} + 1}}{{{{\left( {x + 1} \right)}^2}}} > 0,\forall x \in ( - \infty ; - 1) \cup ( - 1; + \infty )$.
Suy ra hàm số luôn đồng biến trên mỗi khoảng $( - \infty ; - 1),( - 1; + \infty )$.
Do đó: Giá trị lớn nhất trên đoạn $\left[ {0;1} \right]$ là: $y(1) = \dfrac{{{m^2} - 1}}{{1 + 1}} = 4 \Leftrightarrow {m^2} = 9 \Leftrightarrow m = \pm 3.$
Giá trị lớn nhất của hàm số $y = x - \dfrac{1}{x}$ trên $\left( { - \infty ; - 1} \right]$ là:
Ta có : $y' = 1 + \dfrac{1}{{{x^2}}} > 0,\forall x \in \left( { - \infty ; - 1} \right]$.
Suy ra hàm số $y = x - \dfrac{1}{x}$ đồng biến trên $\left( { - \infty ; - 1} \right]$.
Vậy giá trị lớn nhất của hàm số là $y( - 1) = 0$.
Cho hàm số \(y = f\left( x \right)\) có $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0$ và $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty $. Mệnh đề nào sau đây là đúng?
Vì $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0$ và $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty $ nên đồ thị hàm số chỉ một tiệm cận ngang là trục hoành.
Cho hàm số \(\left( C \right):y = \dfrac{{x - 2}}{{x + 1}}\). Đường thẳng \(d:y = x + m\) với $m<0$ cắt đồ thị \(\left( C \right)\) tại hai điểm \(A,B\) phân biệt và \(AB = 2\sqrt 2 \) khi \(m\) nhận giá trị nào trong các giá trị sau đây?
Phương trình hoành độ giao điểm:
\(\dfrac{{x - 2}}{{x + 1}} = x + m \Rightarrow x - 2 = {x^2} + \left( {m + 1} \right)x + m \Rightarrow {x^2} + mx + m + 2 = 0,x \ne - 1\)
Phương trình có \(2\) nghiệm phân biệt \( \Leftrightarrow \Delta = {m^2} - 4m - 8 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2 + 2\sqrt 3 \\m < 2 - 2\sqrt 3 \end{array} \right.\) $\Leftrightarrow m < 2 - 2\sqrt 3$ (vì $m<0$)
Với \(A\left( {{x_1};{x_1} + m} \right),B\left( {{x_2};{x_2} + m} \right)\) thì \(AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}} = \sqrt {2{{\left( {{x_2} - {x_1}} \right)}^2}} \) với \(\left\{ \begin{array}{l}{x_1} + {x_2} = - m\\{x_1}{x_2} = m + 2\end{array} \right.\)
Mà \(AB = 2\sqrt 2 \) nên \(\sqrt {2{{\left( {{x_2} - {x_1}} \right)}^2}} = 2\sqrt 2 \Leftrightarrow 2{\left( {{x_2} - {x_1}} \right)^2} = 8\) \( \Leftrightarrow x_2^2 - 2{x_2}{x_1} + x_1^2 = 4\) \( \Leftrightarrow {\left( {{x_2} + {x_1}} \right)^2} - 4{x_2}{x_1} = 4\) \( \Rightarrow {m^2} - 4\left( {m + 2} \right) = 4\) \( \Leftrightarrow {m^2} - 4m - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 6(L)\\m = - 2(TM)\end{array} \right.\)
Tìm giá trị của tham số $m$ sao cho đồ thị của hàm số $y = {x^3} - 3{x^2} + m$ nhận điểm $A\left( {1;3} \right)$ làm tâm đối xứng.
Ta có: \(y' = 3{x^2} - 6x \Rightarrow y'' = 6x - 6\); \(y'' = 0 \Leftrightarrow x = 1 \Rightarrow y = m - 2\).
Do \(A\left( {1;3} \right)\) là điểm uốn \( \Rightarrow m - 2 = 3 \Leftrightarrow m = 5\) .
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Số đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) là:
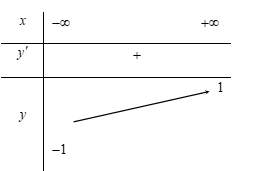
Theo định nghĩa tiệm cận ngang thì đồ thị hàm số có 2 đường tiệm cận ngang là \(y = \pm 1\).
Cho hàm số \(y = {x^3} - 3x\) có giá trị cực đại và cực tiểu lần lượt là \({y_1},{\rm{ }}{y_2}.\) Khi đó:
Ta có: $y' = 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 & \\x = 1 & \end{array} \right.$
Với $x = - 1$ thì $y = 2 = {y_1}$ là giá trị cực đại của hàm số.
Với $x = 1$ thì $y = - 2 = {y_2}$ là giá trị cực tiểu của hàm số.
Vậy ${y_1} - {y_2} = 4$
Cho hàm số \(y = \left( {x - 1} \right){\left( {x + 2} \right)^2}.\) Trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số nằm trên đường thẳng nào dưới đây?
Ta có \(y = {x^3} + 3{x^2} - 4 \Rightarrow y' = 3{x^2} + 6x \Rightarrow y'' = 6x + 6\); \(y'' = 0 \Leftrightarrow x = - 1\)
Vứi \(x = - 1\) thì \(y = - 2\). Vậy \(M\left( { - 1; - 2} \right)\) là trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số. Mà \(M\left( { - 1; - 2} \right) \in d:2x + y + 4 = 0\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đồ thị \(\left( C \right)\) như hình vẽ bên.
Khẳng định nào sau đây là đúng?
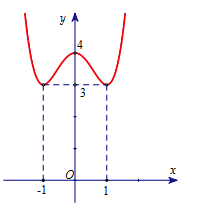
Quan sát đồ thị ta có \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \) nên ta loại đáp án B. Đồ thị hàm số có ba điểm cực trị \(A\left( {0;4} \right),B\left( {1;3} \right),C\left( { - 1;3} \right)\) trong đó có $1$ cực đại và $2$ điểm cực tiểu nên ta loại câu D.
Ngoài ra giá trị cực đại của hàm số là $4$ nên loại C.
Cho hàm số \(y = {x^3} + 5x + 7\). Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 5;\;0} \right]\) bằng bao nhiêu?
\(y' = 3{x^2} + 5 > 0;\forall x \in \left[ { - 5;\;0} \right]\)\( \Rightarrow \mathop {\max }\limits_{\left[ { - 5;\;0} \right]} y = y\left( 0 \right) = 7\).
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\). Biết \(f\left( {x + 1} \right) = {x^3} + 3{x^2} + 3x + 2\). Hãy xác định biểu thức \(f\left( x \right)\).
Đặt \(t = x + 1 \Leftrightarrow x = t - 1\) . Khi đó
\(f\left( t \right) = {\left( {t - 1} \right)^3} + 3{\left( {t - 1} \right)^2} + 3\left( {t - 1} \right) + 2 = {t^3} + 1\) hay \(f\left( x \right) = {x^3} + 1\).
Biết rằng đồ thị hàm số \(y = \dfrac{{x + 3}}{{x - 1}}\) và đường thẳng \(y = x - 2\) cắt nhau tại hai điểm phân biệt \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\). Tính \({y_A} + {y_B}\).
Phương trình hoành độ giao điểm: \(x - 2 = \dfrac{{x + 3}}{{x - 1}} \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\{x^2} - 4x - 1 = 0{\rm{ }}\left( 1 \right)\end{array} \right.\)
Ta có \({y_A} + {y_B} = {x_A} + {x_B} - 4\) mà\({x_A},{x_B}\) là nghiệm phương trình \(\left( 1 \right)\) nên \({x_A} + {x_B} = 4.\)
Vậy \({y_A} + {y_B} = 0\).
Số giao điểm của đường cong \(y = {x^3} - 3{x^2} + x - 1\) và đường thẳng \(y = 1 - 2x\) bằng:
Xét phương trình hoành độ:
\({x^3} - 3{x^2} + x - 1 = 1 - 2x\) \( \Leftrightarrow {x^3} - 3{x^2} + 3x - 2 = 0\) \( \Leftrightarrow \left( {x - 2} \right)\left( {{x^2} - x + 1} \right) = 0\) \( \Leftrightarrow x = 2\)
Vậy số giao điểm là \(1\).
Hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 1} \right)^2}\left( {x - 3} \right)\) . Phát biểu nào sau đây là đúng ?
\(f'\left( x \right) = {\left( {x - 1} \right)^2}\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\).
Từ đó ta có bảng biến thiên như sau:
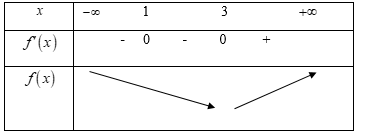
Từ bảng biến thiên ta thấy hàm số có \(1\) điểm cực trị duy nhất.
