Tìm tất cả các tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{\left| x \right|}}{{\sqrt {{x^2} - 1} }}\).
Ta có: $\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{\left| x \right|}}{{\sqrt {{x^2} - 1} }} = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{\left| x \right|}}{{\left| x \right|\sqrt {1 - \dfrac{1}{{{x^2}}}} }} = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{1}{{\sqrt {1 - \dfrac{1}{{{x^2}}}} }} = 1$.
Suy ra tiệm cận ngang \(y = 1\).
Đồ thị hàm số \(y = \dfrac{{\left( {2m + 1} \right)x + 3}}{{x + 1}}\) có đường tiệm cận đi qua điểm \(A\left( { - 2;7} \right)\) khi và chỉ khi
Đồ thị hàm số có đường tiệm cận \( \Leftrightarrow 2m - 2 \ne 0\)\( \Leftrightarrow m \ne 1\).
Đồ thị hàm số có đường tiệm cận đứng \(x = - 1\) và tiệm cận ngang \(y = 2m + 1\).
Do đó đường tiệm cận đi qua điểm \(A\left( { - 2;\;7} \right) \Leftrightarrow 2m + 1 = 7 \Leftrightarrow m = 3\).(thỏa mãn)
Biết đồ thị hàm số $y = a{x^3} + b{x^2} + cx + d$ có 2 điểm cực trị là $\left( { - 1;18} \right)$ và $\left( {3; - 16} \right).$ Tính $a + b + c + d.$
\(y = a{x^3} + b{x^2} + cx + d \Rightarrow {y^,} = 3a{x^2} + 2bx + c = 0\) có 2 nghiệm \({x_1} + {x_2} = \dfrac{{ - 2b}}{{3a}} = - 1 + 3 \Rightarrow b = - 3a\left( 1 \right)\);
\({x_1}.{x_2} = \dfrac{c}{{3a}} = - 1.3 \Rightarrow c = - 9a\left( 2 \right)\)
Mà 2 điểm cực trị là \(( - 1;18)\) và \((3; - 16)\) thuộc đồ thị nên ta có:
\( - a + b - c + d = 18\left( 3 \right)\)
\(27a + 9b + 3c + d = - 16\left( 4 \right)\).
Giải hệ 4 phương trình\(\left( 1 \right)\),\(\left( 2 \right)\),\(\left( 3 \right)\),\(\left( 4 \right)\) ta có:
\(a = \dfrac{{17}}{{16}}\),\(b = \dfrac{{ - 51}}{{16}}\),\(c = \dfrac{{ - 153}}{{16}}\),\(d = \dfrac{{203}}{{16}}\)\( \Rightarrow a + b + c + d = 1\)
Tìm tất cả các giá trị của \(m\) để hàm số \(f\left( x \right) = \dfrac{{mx + 1}}{{x - m}}\) có giá trị lớn nhất trên \(\left[ {1;\;2} \right]\) bằng \( - 2\).
Tập xác định: \(D = \mathbb{R}\backslash \left\{ m \right\}\)\( \Rightarrow m \notin \left[ {1;\;2} \right]\).
\(f'\left( x \right) = \dfrac{{ - {m^2} - 1}}{{{{\left( {x - m} \right)}^2}}} < 0;\forall x \ne m\)\( \Rightarrow \mathop {\max }\limits_{\left[ {1;\;2} \right]} f\left( x \right) = f\left( 1 \right) = \dfrac{{m + 1}}{{1 - m}}\)
Theo đề bài \(\mathop {\max }\limits_{\left[ {1;\;2} \right]} f\left( x \right) = - 2 \Leftrightarrow \dfrac{{m + 1}}{{1 - m}} = - 2 \Leftrightarrow m + 1 = 2m - 2 \Leftrightarrow m = 3\)
Tìm tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = {x^4} - 2m{x^2} + 2m - 4\) đi qua điểm \(N\left( { - 2;0} \right).\)
Đồ thị hàm số đi qua điểm $N\left( { - 2;0} \right)$.
Ta có $0 = {\left( { - 2} \right)^4} - 2m{\left( { - 2} \right)^2} + 2m - 4 \Leftrightarrow m = 2$
Cho hàm số \(y = {x^3} - 3x + 2\) có đồ thị bên dưới. Khi đó giá trị \(m\) để phương trình \( - {x^3} + 3x - 5m + 1 = 0\) có $3$ nghiệm phân biệt, trong đó có $2$ nghiệm âm và một nghiệm dương là
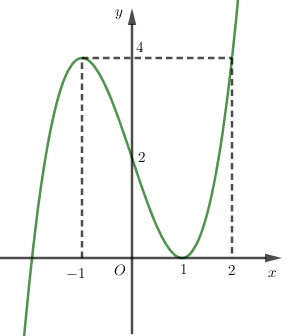
Ta có: \( - {x^3} + 3x - 5m + 1 = 0 \Leftrightarrow - 5m + 3 = {x^3} - 3x + 2\).
Phương trình có hai nghiệm âm một nghiệm dương \( \Leftrightarrow 2 < - 5m + 3 < 4 \Leftrightarrow - \dfrac{1}{5} < m < \dfrac{1}{5}\).
Hình vẽ bên là đồ thị hàm trùng phương. Giá trị $m$ để phương trình \(\left| {f\left( x \right)} \right| = m\) có 4 nghiệm đôi một khác nhau là:
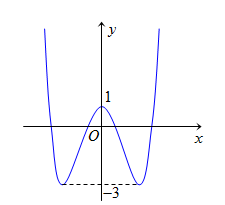
Đồ thị \(y = \left| {f\left( x \right)} \right|\) là:
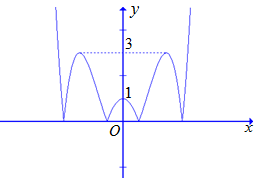
Phương trình có $4$ nghiệm phân biệt \( \Leftrightarrow m = 0\) hoặc \(m = 3\).
Một nhà máy cần thiết kế một chiếc bể đựng nước hình trụ bằng tôn có nắp, có thể tích là \(64\pi \left( {{m^3}} \right)\). Tìm bán kính đáy \(r\) của hình trụ sao cho hình trụ được làm ra tốn ít nhiên liệu nhất.
Gọi hình trụ có chiều cao \(h\), bán kính đáy \(r\).
Ta có: \(V = \pi {r^2}h \Rightarrow h = \dfrac{{64\pi }}{{\pi {r^2}}} = \dfrac{{64}}{{{r^2}}}\)
Để tốn ít nhiên liệu nhất thì diện tích toàn phần nhỏ nhất.
Ta có: \({S_{tp}} = 2{S_{day}} + {S_{xq}} = 2\pi {r^2} + 2\pi rh = 2\pi {r^2} + \dfrac{{128\pi }}{r}\).
Xét hàm số \(f\left( r \right) = 2\pi {r^2} + \dfrac{{128\pi }}{r}\) với \(r > 0\).
Ta có \(f'\left( r \right) = 4\pi r - \dfrac{{128\pi }}{{{r^2}}};f'\left( r \right) = 0 \Leftrightarrow r = \sqrt[3]{{32}}\,\).
Lập bảng biến thiên ta có \(f\left( r \right)\) đạt GTNN khi \(r = \sqrt[3]{{32}}\).
