Câu hỏi:
2 năm trước
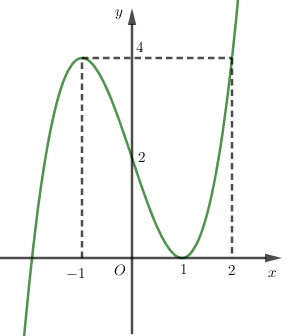
Cho hàm số \(y = {x^3} - 3x + 2\) có đồ thị bên dưới. Khi đó giá trị \(m\) để phương trình \( - {x^3} + 3x - 5m + 1 = 0\) có $3$ nghiệm phân biệt, trong đó có $2$ nghiệm âm và một nghiệm dương là
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có: \( - {x^3} + 3x - 5m + 1 = 0 \Leftrightarrow - 5m + 3 = {x^3} - 3x + 2\).
Phương trình có hai nghiệm âm một nghiệm dương \( \Leftrightarrow 2 < - 5m + 3 < 4 \Leftrightarrow - \dfrac{1}{5} < m < \dfrac{1}{5}\).
Hướng dẫn giải:
- Biến đổi phương trình về dạng \( - 5m + 3 = {x^3} - 3x + 2\).
- Phương trình đã cho có \(3\) nghiệm phân biệt trong đó có hai nghiệm âm, một nghiệm dương \( \Leftrightarrow \) đường thẳng \(y = - 5m + 3\) cắt đồ thị hàm số đã cho tại ba điểm thỏa mãn \(2\) điểm có hoành độ âm và \(1\) điểm có hoành độ dương.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
