Lực hướng tâm

Ta có:

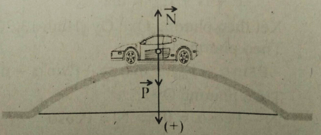
+ Hợp lực tác dụng lên ô tô: \(\overrightarrow F  = \overrightarrow P  + \overrightarrow N \)

+ Chiếu lên phương hướng tâm, ta được: \({F_{ht}} = P - N = m\dfrac{{{v^2}}}{r}\)

Ta suy ra:

\(N = P - m\dfrac{{{v^2}}}{r} = mg - m\dfrac{{{v^2}}}{r}\)

\( \leftrightarrow N = 1000.10 - 1000.\dfrac{{{{10}^2}}}{{50}} = 8000(N)\)

Ta có:

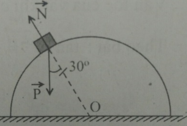
+ Hợp lực tác dụng lên ô tô: \(\overrightarrow F  = \overrightarrow P  + \overrightarrow N \)

+ Chiếu lên phương hướng tâm, ta được:

\({F_{ht}} = P.c{\rm{os30 - N = m}}\dfrac{{{v^2}}}{r}\)

\( \to N = P.c{\rm{os30}} - {\rm{m}}\dfrac{{{v^2}}}{r} = mgc{\rm{os30}} - {\rm{m}}\dfrac{{{v^2}}}{r}\)

=\(1000.10.c{\rm{os30 - 1000}}\dfrac{{{{10}^2}}}{{50}} = 6660,25(N)\)

Gia tốc rơi tự do ở độ cao h=0,5R là:

\(g' = \dfrac{{GM}}{{{{(R + 0,5{\rm{R}})}^2}}} = \dfrac{4}{9}\dfrac{{GM}}{{{R^2}}} = \dfrac{4}{9}g = \dfrac{4}{9}.10 = \dfrac{{40}}{9}m/{s^2}\)

Mặt khác, ta có: \(g' = \dfrac{{{v^2}}}{r} \to v = \sqrt {rg'}  = \sqrt {(6400 + 0,5.6400).1000.\dfrac{{40}}{9}}  = 6532m/s\)

Gia tốc rơi tự do ở độ cao h=R là:

\(g' = \dfrac{{GM}}{{{{(R + {\rm{R}})}^2}}} = \dfrac{1}{4}\dfrac{{GM}}{{{R^2}}} = \dfrac{1}{4}g = \dfrac{1}{4}.10 = \dfrac{{10}}{4}m/{s^2}\)

\(g' = \dfrac{{{v^2}}}{r} \to v = \sqrt {rg'}  = \sqrt {(6400 + 6400).1000.\dfrac{{10}}{4}}  = 5657m/s\)

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

Khi đó:

\({F_{hd}} = {F_{ht}} = m\dfrac{{{v^2}}}{r}\)

\({F_{h{\rm{d}}}} = {F_{ht}} = m\dfrac{{{v^2}}}{r} = 600.\dfrac{{{{5657}^2}}}{{6400.1000.2}} = 1500(N)\)

Ta có, lực hấp dẫn đóng vai trò lực hướng tâm:

\({{\rm{F}}_{h{\rm{d}}}} = {F_{ht}} = m\dfrac{{{v^2}}}{r} = m\dfrac{{{v^2}}}{{2,5R}} = 800.\dfrac{{{{5009}^2}}}{{2,5.6400000}} = 1254,5N\)

\(T = \dfrac{{2\pi }}{\omega }\) mà \(v = \omega r = \omega .2,5R \to \omega  = \dfrac{v}{{2,5R}}\)

\(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{\dfrac{v}{{2,5R}}}} = \dfrac{{5\pi R}}{v} = \dfrac{{5\pi .6400000}}{{5009}} = 20060{\rm{s}}\)

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

\({F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}} \)

Với: \(r = R + h = R + \dfrac{3}{2}R = 2,5R\)

Nên:\(v = \sqrt {\dfrac{{GM}}{{2,5{\rm{R}}}}} \)

Mặt khác: Gia tốc rơi tự do của vật ở mặt đất: \(g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}\)\(v = \sqrt {\dfrac{{g{R^2}}}{{2,5{\rm{R}}}}}  = \sqrt {\dfrac{{gR}}{{2,5}}}  = \sqrt {\dfrac{{9,8.6400000}}{{2,5}}}  = 5009m/s\)

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

\({F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}} \)

Với: \(r = R + h = R + \dfrac{3}{2}R = 2,5R\)

Nên:\(v = \sqrt {\dfrac{{GM}}{{2,5{\rm{R}}}}} \)

Mặt khác: Gia tốc rơi tự do của vật ở mặt đất: \(g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}\)\(v = \sqrt {\dfrac{{g{R^2}}}{{2,5{\rm{R}}}}}  = \sqrt {\dfrac{{gR}}{{2,5}}}  = \sqrt {\dfrac{{9,8.6400000}}{{2,5}}}  = 5009m/s\)

Chu kì chuyển động của Mặt Trăng quanh Trái Đất là : \({T_1} = \dfrac{{365}}{{13}} = 28\)(ngày)

Chu kì chuyển động của Trái Đất  quanh Mặt Trời là:\({T_2} = 365\)( ngày)

Khi Mặt Trăng chuyển động tròn quanh Trái Đất thì lực hấp dẫn giữa Mặt Trăng và Trái Đất đóng vai trò là lực hướng tâm, nên:

\({F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Leftrightarrow \dfrac{{GM}}{r} = {v^2}\)

Mà: \(v = \omega r = \dfrac{{2\pi }}{T}r\)

\( \leftrightarrow \dfrac{{GM}}{{{r_1}}} = \dfrac{{4{\pi ^2}}}{{{T_1}^2}}{r_1}^2 \to M = \dfrac{{4{\pi ^2}}}{{{T_1}^2G}}{r_1}^3\)

Khi Trái Đất chuyển động tròn quanh Mặt Trời thì lực hấp dẫn giữa Trái Đất và Mặt Trời  đóng vai trò là lực hướng tâm, nên:

\({F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Leftrightarrow \dfrac{{GM}}{r} = {v^2}\)

Mà: \(v = \omega r = \dfrac{{2\pi }}{T}r\)

\( \leftrightarrow \dfrac{{G{M_{mt}}}}{{{r_2}}} = \dfrac{{4{\pi ^2}}}{{{T_2}^2}}{r_2}^2 \to {M_{mt}} = \dfrac{{4{\pi ^2}}}{{{T_2}^2G}}{r_2}^3\)

Tỉ số khối lượng của Mặt Trời và Trái Đất

\(\dfrac{{{M_{mt}}}}{M} = \dfrac{{\dfrac{{4{\pi ^2}}}{{{T_2}^2G}}{r_2}^3}}{{\dfrac{{4{\pi ^2}}}{{{T_1}^2G}}{r_1}^3}} = \dfrac{{{T_1}^2{r_2}^3}}{{{T_2}^2{r_1}^3}} = {(\dfrac{{{T_1}}}{{{T_2}}})^2}.{(\dfrac{{{r_2}}}{{{r_1}}})^3} = {(\dfrac{{28}}{{365}})^2}.{(390)^3} \approx {350.10^3}\)(lần)

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

\({F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}} \)

Với:\(r = R + h = R + \dfrac{7}{9}R = \dfrac{{16{\rm{R}}}}{9}\)

Nên:\(v = \sqrt {\dfrac{{GM}}{{\dfrac{{16{\rm{R}}}}{9}}}}  = \dfrac{3}{4}\sqrt {\dfrac{{GM}}{R}} \)

Mặt khác: Gia tốc rơi tự do của vật ở mặt đất: \(g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}\)

\(v = \sqrt {\dfrac{{g{R^2}}}{{\dfrac{{16{\rm{R}}}}{9}}}}  = \sqrt {\dfrac{{9gR}}{{16}}}  = \sqrt {\dfrac{{9.10.6400000}}{{16}}}  = 6000m/s\)

Ta có:

\(T = \dfrac{{2\pi }}{\omega }\) mà\(v = \omega .r = \omega .\dfrac{{16{\rm{R}}}}{9} \to \omega  = \dfrac{{9v}}{{16R}}\)

\(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{\dfrac{{9v}}{{16R}}}} = \dfrac{{32\pi R}}{{9v}} = \dfrac{{32\pi 6400000}}{{9.6000}} = 11914,8s=3,3h\)

Vậy chu kì chuyển động của vệ tinh là: 3,3 giờ.

Ta có:

+ \(f = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }} \to \omega  = 2\pi f\)

+ Lực hướng tâm tác dụng vào vật: \({F_{ht}} = m{\omega ^2}r = m{\left( {2\pi f} \right)^2}r\)

+ Để vật không văng ra khỏi mặt bàn, ta phải có:

\(\begin{array}{l}F = {F_{m{\rm{s}}n}}_{\left( {{\rm{max}}} \right)} \leftrightarrow m{\left( {2\pi f} \right)^2}r = {F_{m{\rm{s}}n}}_{\left( {{\rm{max}}} \right)}\\ \to {f^2} = \dfrac{{{F_{m{\rm{s}}n}}_{\left( {{\rm{max}}} \right)}}}{{m4{\pi ^2}r}} = \dfrac{{0,08}}{{{{20.10}^{ - 3}}.4{\pi ^2}.1}} = 0,101\\ \to f \approx 0,32{s^{ - 1}}\end{array}\)

Vậy muốn vật không bị văng ra khỏi mặt bàn thì tần số quay của bàn lớn nhất là: \(f = 0,32{{\rm{s}}^{ - 1}}\)

=> Chu kì nhỏ nhất là: \({T_{\min }} = \dfrac{1}{{{f_{{\rm{max}}}}}} = \dfrac{1}{{0,32}} = 3,15{\rm{s}}\)

Khi hòn đá ở điểm thấp nhất của quỹ đạo thì trọng lượng và lực căng dây đóng vai trò là lực hướng tâm.

\({{\rm{F}}_{ht}} = P + T \to T = {F_{ht}} - P = m{\omega ^2}r - mg = 0,{4.8^2}.0,5 - 0,4.10 = 8,8N\)

Ta có:\(\omega  = 2\pi f\)

Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm:

Khi trục \(\Delta \) quay thì lò xo dãn một đoạn \(\Delta l\)

\( \to {F_{ht}} = {F_{dh}} \leftrightarrow m{\omega ^2}({l_0} + \Delta l) = k\Delta l\)

\( \to \Delta l(k - m{\omega ^2}) = m{\omega ^2}{l_0}\)

\( \to \Delta l = \dfrac{{m{\omega ^2}{l_0}}}{{k - m{\omega ^2}}}\)

Vậy chiều dài của lò xo khi quay: \(l = {l_0} + \Delta l\)

Lực hướng tâm: \({F_{ht}} = m{a_{ht}} = \dfrac{{m{v^2}}}{r} = m.{\omega ^2}r\)

A, C, D - đúng

B - sai vì: Không phải xe chuyển động vào một đoạn đường cong lực đóng vai trò hướng tâm luôn là lực ma sát.

Ta có: Lực (hay hợp lực của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm gọi là lực hướng tâm.

=> Các phương án:

A - sai vì vật có thể chịu tác dụng của nhiều lực

B - đúng

C - sai vì lực hướng tâm không phải là lực mới

D - sai vì hợp lực của tất cả các lực tác dụng lên vật hướng vào tâm

Lực (hay hợp lực của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm gọi là lực hướng tâm.

Có lực hướng tâm khi vật chuyển động cong

từ biểu thức tính lực hướng tâm: \({F_{ht}} = m{a_{ht}} = m\frac{{{v^2}}}{r} = m{\omega ^2}r\)

Ta suy ra, khi bán kính quỹ đạo tăng gấp 2 lần so với trước và giảm tốc độ quay còn một nửa thì so với ban đầu, lực hướng tâm giảm đi 2 lần.

Ta có, lực hướng tâm: \({F_{ht}} = m{a_{ht}} = m\frac{{{v^2}}}{r}\)

Thay số ta được: \({F_{ht}} = 0,15\frac{{{2^2}}}{{1,5}} = 0,4N\)