Lực hướng tâm

Ta có: \(\left\{ \begin{array}{l}m = 200g = 0,2kg\\r = 50cm = 0,5m\\{F_{ht}} = 10N\end{array} \right.\)

Lực hướng tâm tác dụng lên vật:

\({F_{ht}} = m{\omega ^2}r \Rightarrow \omega  = \sqrt {\dfrac{{{F_{ht}}}}{{mr}}}  = \sqrt {\dfrac{{10}}{{0,2.0,5}}}  = 10rad/s\)

Độ lớn của lực hướng tâm của chiếc xe:

\({F_{ht}} = m.\dfrac{{{v^2}}}{r} = 1200.\dfrac{{{{50}^2}}}{{250}} = 12000N\)

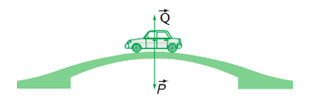
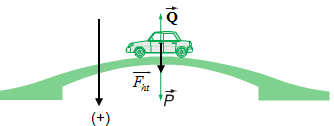
Xét chuyển động tròn đều của ô tô. Ta có :

\(\overrightarrow Q  + \overrightarrow P  = \overrightarrow {{F_{ht}}} \,\,\,\left( * \right)\)

Chiếu biểu thức  (*) lên phương bán kính hướng vào tâm ta được :

\( - Q + P = {F_{ht}} \Rightarrow Q = P - {F_{ht}} = mg - \dfrac{{m{v^2}}}{R}\)

Mặt khác áp lực \(N\) luôn bằng phản lực \(Q\)

→ Áp lực của ô tô lên mặt cầu lúc này bằng :

\(N = Q = mg - \dfrac{{m{v^2}}}{R} = 1500.10 - 1500.\dfrac{{{{15}^2}}}{{25}} = 1500N\)

+  Lực đóng vai trò lực hướng tâm giữ vệ tinh chuyển động tròn đều quanh Trái đất chính là lực hấp dẫn giữa Trái Đất và vệ tinh:

\(\begin{array}{l}{F_{hd}} = {F_{ht}} \Leftrightarrow G.\dfrac{{m.M}}{{{{(R + h)}^2}}} = m.\dfrac{{{v^2}}}{R} \Leftrightarrow \dfrac{{GM}}{{(R + h)}} = {v^2}\\ \Rightarrow v = \sqrt {\dfrac{{GM}}{{R + h}}}  = \sqrt {\dfrac{{6,{{67.10}^{ - 11}}{{.6.10}^{24}}}}{{6\,400\,000 + 1600\,000}}} \\ \Rightarrow v = 7072,84m/s\end{array}\)

+ Ta có:

\(\begin{array}{l}v = r.\omega  = r.\dfrac{{2\pi }}{T} \Rightarrow T = \dfrac{{2\pi (R + h)}}{v}\\ \Rightarrow T = \dfrac{{2\pi .(6400000 + 1600000)}}{{7072,84}} = 7106,83s\end{array}\)

Gọi \(h\) là khoảng cách từ bề mặt Trái Đất đến vệ tinh.

Lực hấp dẫn đóng vai trò là lực hướng tâm:

\( \Rightarrow {F_{ht}} = P = 920N \Leftrightarrow m{\omega ^2}r = 920N\)

Gọi h là khoảng cách từ bề mặt Trái Đất đến vệ tinh \( \Rightarrow r = R + h\)

\(\begin{array}{l} \Rightarrow m\dfrac{{4{\pi ^2}}}{{{T^2}}}.\left( {R + h} \right) = 920N\\ \Rightarrow R + h = \dfrac{{920.{T^2}}}{{4{\pi ^2}.m}} \Rightarrow h = \dfrac{{920.{T^2}}}{{4{\pi ^2}.m}} - R\end{array}\)

Với: \(\left\{ \begin{array}{l}T = 5,{3.10^3}s\\m = 100kg\\R = 6400km = 6400000m\end{array} \right.\)

\(\begin{array}{l} \Rightarrow h = \dfrac{{920.{{\left( {5,{{3.10}^3}} \right)}^2}}}{{4{\pi ^2}.100}} - 6\,400\,000\\\,\,\,\,\,\,\,\,\,\, = 152699,9m \approx 153km\end{array}\)

Vật đi được \(120\) vòng trong \(1\) phút \((60s)\)

\( \Rightarrow \) Vật đi được \(1\) vòng trong: \(\dfrac{{60}}{{120}} = 0,5s\)

\( \Rightarrow \) Chu kì: \(T = 0,5s\)

\( \Rightarrow \) Tần số góc: \(\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,5}} = 4\pi \,\left( {rad/s} \right)\)

Ta có: \(\left\{ \begin{array}{l}m = 300g = 0,3kg\\r = 10cm = 0,1m\\\omega  = 4\pi \,\left( {rad/s} \right)\end{array} \right.\)

Độ lớn lực hướng tâm:

\({F_{ht}} = m.{a_{ht}} = m.R.\omega ^2 = 0,3.0,1.\left ( 4\pi  \right )^2 = 4,8N\)

Lực đóng vai trò lực hướng tâm là hợp lực của trọng lực tác dụng lên vật, phản lực của đĩa và lực ma sát nghỉ.

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

\({F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}} \)

Với: \(r = R + h = R + R = 2R\)

Nên: \(v = \sqrt {\dfrac{{GM}}{{2R}}} \)

Mặt khác:

Gia tốc rơi tự do của vật ở mặt đất: \(g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}\)

\( \Rightarrow v = \sqrt {\dfrac{{g{R^2}}}{{2R}}}  = \sqrt {\dfrac{{gR}}{2}}  = \sqrt {\dfrac{{9,8.6400000}}{2}}  \\= 5600{\rm{ m/s}} = 5,6{\rm{ km/s}}\)

Ta có, lực hấp dẫn đóng vai trò lực hướng tâm:

\({F_{hd}} = {F_{ht}} = \dfrac{{m{v^2}}}{r} = \dfrac{{m{v^2}}}{{2R}} \\= \dfrac{{{{600.5600}^2}}}{{2.6400000}} = 1470{\rm{ N}}\)

\(T = \dfrac{{2\pi }}{\omega }\)

Mà

\(v = \omega r = \omega (2R) \\\Rightarrow \omega  = \dfrac{v}{{2R}}\)

\( \Rightarrow T = \dfrac{{2\pi }}{{\dfrac{v}{{2R}}}}= \dfrac{{4\pi R}}{v} \\= \dfrac{{4\pi .6400000}}{{5600}} \approx 14362{\rm{ s}}\)

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

\({F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}} \)

Với: \(r = R + h = R + R = 2R\)

Nên: \(v = \sqrt {\dfrac{{GM}}{{2R}}} \)

Mặt khác:

Gia tốc rơi tự do của vật ở mặt đất: \(g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}\)

\( \Rightarrow v = \sqrt {\dfrac{{g{R^2}}}{{2R}}}  = \sqrt {\dfrac{{gR}}{2}}  = \sqrt {\dfrac{{9,8.6400000}}{2}}  \\= 5600{\rm{ m/s}} = 5,6{\rm{ km/s}}\)

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

\({F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}} \)

Với: \(r = R + h = R + R = 2R\)

Nên: \(v = \sqrt {\dfrac{{GM}}{{2R}}} \)

Mặt khác:

Gia tốc rơi tự do của vật ở mặt đất: \(g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}\)

\( \Rightarrow v = \sqrt {\dfrac{{g{R^2}}}{{2R}}}  = \sqrt {\dfrac{{gR}}{2}}  = \sqrt {\dfrac{{9,8.6400000}}{2}}  \\= 5600{\rm{ m/s}} = 5,6{\rm{ km/s}}\)

Lực hướng tâm: \({F_{ht}} = m{a_{ht}} = \dfrac{{m{v^2}}}{r} = m.{\omega ^2}r\)

A - sai vì vệ tinh nhân tạo chuyển động tròn đều quanh Trái Đất do lực hấp dẫn đóng vai trò lực hướng tâm

B, C, D - đúng.

Ở những đoạn đường vòng, mặt đường được nâng lên một bên. Việc làm này nhằm mục đích tăng lực ma sát để khỏi trượt.

Lực (hay hợp lực của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm gọi là lực hướng tâm.

A, B, C - đúng.

D - sai: vì lực ma sát giúp cho ô-tô qua khúc quanh an toàn.

Có lực hướng tâm khi vật chuyển động cong.

Từ biểu thức tính lực hướng tâm: \({F_{ht}} = m{a_{ht}} = m\dfrac{{{v^2}}}{r} = m{\omega ^2}r\)

Ta suy ra, khi bán kính quỹ đạo giảm xuống 2 lần so với trước và đồng thời tăng tốc độ quay lên gấp đôi thì so với ban đầu, lực hướng tâm tăng lên 2 lần.

Ta có, lực hướng tâm: \({F_{ht}} = m{a_{ht}} = m\dfrac{{{v^2}}}{r}\)

Thay số ta được:\({F_{ht}} = 0,25.\dfrac{{0,{5^2}}}{{0,3}} = 0,208N\)

+ Tần số:\(f = \dfrac{{72}}{{60}} = 1,2(Hz)\)

+ Tốc độ góc:\(\omega  = 2\pi f = 2\pi .1,2 = 2,4\pi (ra{\rm{d}}/s)\)

+ Ta có độ lớn lực ma sát nghỉ của bàn tác dụng lên vật đóng vai trò như lực hướng tâm:

\(F = m{\omega ^2}r = 0,2.{(2,4\pi )^2}.0,4 = 4,54(N)\)