Lực hướng tâm

+ Tần số: $f = \frac{{120}}{{60}} = 2\left( {H{\rm{z}}} \right)$

+ Tốc độ góc: $\omega  = 2\pi f = 2\pi .2 = 4\pi \left( {ra{\rm{d}}/s} \right)$

+ Ta có, lực hướng tâm: ${F_{ht}} = m{\omega ^2}r = 0,25{\left( {4\pi } \right)^2}1,2 \approx 47,3N$

Ta có:

+ Hợp lực tác dụng lên ô tô: $\overrightarrow F  = \overrightarrow P  + \overrightarrow N$

+ Chiếu lên phương hướng tâm, ta được: ${F_{ht}} = P - N = m\frac{{{v^2}}}{r}$

Ta suy ra:

$\begin{array}{l}N = P - m\frac{{{v^2}}}{r} = mg - m\frac{{{v^2}}}{r}\\ = 4000.10 - 4000\frac{{{{20}^2}}}{{100}} = 24000N\end{array}$

Ta có:

+ Hợp lực tác dụng lên ô tô: $\overrightarrow F  = \overrightarrow P  + \overrightarrow N$

+ Chiếu lên phương hướng tâm, ta được:

$\begin{array}{l}{F_{ht}} = Pc{\rm{os3}}{{\rm{0}}^0} - N = m\frac{{{v^2}}}{r}\\ \to N = Pc{\rm{os3}}{{\rm{0}}^0} - m\frac{{{v^2}}}{r} = mgc{\rm{os3}}{{\rm{0}}^0} - m\frac{{{v^2}}}{r}\\ = 2500.10.c{\rm{os3}}{{\rm{0}}^0} - 2500\frac{{{{15}^2}}}{{1000}} = 21088N\end{array}$

Ta có:

+ Tốc độ góc: $\omega  = \frac{{2\pi }}{T}$

+ Lực hướng tâm: ${F_{ht}} = m\frac{{{v^2}}}{r} = m{\omega ^2}r$

=> Ta suy ra:

Độ lớn lực hướng tâm tác dụng lên vệ tinh:

${F_{ht}} = m{\omega ^2}r = \frac{{m4{\pi ^2}(R + h)}}{{{T^2}}} = \frac{{100.4.{\pi ^2}.6553.1000}}{{{{({{5.10}^3})}^2}}} \approx 1035{\rm{ N}}$

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

Khi đó:

${F_{hd}} = {F_{ht}} = m\frac{{{v^2}}}{r}$

Với: $r = R + h$ và $v = \omega r = \frac{{2\pi }}{T}(R + h)$

$\Rightarrow {F_{hd}} = {F_{ht}} = m{\omega ^2}r = \frac{{m4{\pi ^2}(R + h)}}{{{T^2}}} = \frac{{20.4{\pi ^2}.7400.1000}}{{{{86400}^2}}} \approx 0,783{\rm{ N}}$

Khi Mặt Trăng chuyển động tròn quanh Trái Đất thì lực hấp dẫn giữa Mặt Trăng và Trái Đất đóng vai trò là lực hướng tâm, nên:

${F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Leftrightarrow \dfrac{{GM}}{r} = {v^2}$

Mà: $v = \omega r = \dfrac{{2\pi }}{T}r$

$\Rightarrow \dfrac{{GM}}{r} = \dfrac{{4{\pi ^2}}}{{{T^2}}}{r^2} \Rightarrow M = \dfrac{{4{\pi ^2}{r^3}}}{{{T^2}G}} = \dfrac{{4{\pi ^2}.{{(3,{{84.10}^8})}^3}}}{{{{(27,32.86400)}^2}.6,{{67.10}^{ - 11}}}} \approx {6.10^{24}}{\rm{ kg}}$

- Theo Niutơn thì trọng lực mà Trái Đất tác dụng lên vệ tinh chính là lực hấp dẫn giữa Trái Đất và vệ tinh.

$P = {F_{hd}} = 920{\rm{ N}}$

- Mà: ${F_{hd}} = {F_{ht}} = 920{\rm{ N}}$

${F_{ht}} = m\frac{{{v^2}}}{r} = \frac{{m\frac{{4{\pi ^2}}}{{{T^2}}}{r^2}}}{r} = \frac{{m4{\pi ^2}r}}{{{T^2}}} \Rightarrow r = \frac{{{F_{ht}}{T^2}}}{{m4{\pi ^2}}} = \frac{{920.{{(5,{{3.10}^3})}^2}}}{{100.4{\pi ^2}}} = 6546057,712{\rm{ m}} = 6546,058{\rm{ km}}$

- Mà: $r = R + h \Rightarrow h = r - R = 6546,058 - 6400 = 146,058{\rm{ km}}$

Ta có:

+ $f = \frac{1}{T} = \frac{\omega }{{2\pi }} \to \omega  = 2\pi f$

+ Lực hướng tâm tác dụng vào vật: ${F_{ht}} = m{\omega ^2}r = m{\left( {2\pi f} \right)^2}r$

+ Để vật không văng ra khỏi mặt bàn, ta phải có:

$\begin{array}{l}{F_{ht}} = {F_{m{\rm{s}}n}}_{\left( {{\rm{max}}} \right)} \leftrightarrow m{\left( {2\pi f} \right)^2}r = {F_{m{\rm{s}}n}}_{\left( {{\rm{max}}} \right)}\\ \to {f^2} = \frac{{{F_{m{\rm{s}}n}}_{\left( {{\rm{max}}} \right)}}}{{m4{\pi ^2}r}} = \frac{{0,08}}{{{{20.10}^{ - 3}}.4{\pi ^2}.1}} = 0,101\\ \to f \approx 0,32{s^{ - 1}}\end{array}$

Vậy muốn vật không bị  văng ra khỏi mặt bàn thì tần số quay của bàn lớn nhất là: $f = 0,32{{\rm{s}}^{ - 1}}$   

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

${F_{hd}} = {F_{ht}} \Leftrightarrow G\dfrac{{mM}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}}$

Với: $r = R + h = R + R = 2R$

Nên: $v = \sqrt {\dfrac{{GM}}{{2R}}}$

Mặt khác:

Gia tốc rơi tự do của vật ở mặt đất: $g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}$

$\Rightarrow v = \sqrt {\dfrac{{g{R^2}}}{{2R}}}  = \sqrt {\dfrac{{gR}}{2}}  = \sqrt {\dfrac{{9,8.6400000}}{2}}  \\= 5600{\rm{ m/s}} = 5,6{\rm{ km/s}}$

$T = \dfrac{{2\pi }}{\omega }$

Mà

$v = \omega r = \omega (2R) \\\Rightarrow \omega  = \dfrac{v}{{2R}}$

$\Rightarrow T = \dfrac{{2\pi }}{{\dfrac{v}{{2R}}}}= \dfrac{{4\pi R}}{v} \\= \dfrac{{4\pi .6400000}}{{5600}} \approx 14362{\rm{ s}}$

Ta có, lực hấp dẫn đóng vai trò lực hướng tâm:

${F_{hd}} = {F_{ht}} = \dfrac{{m{v^2}}}{r} = \dfrac{{m{v^2}}}{{2R}} \\= \dfrac{{{{600.5600}^2}}}{{2.6400000}} = 1470{\rm{ N}}$

Khi hòn đá ở điểm thấp nhất của quỹ đạo thì trọng lượng và lực căng dây đóng vai trò là lực hướng tâm.

${{\rm{F}}_{ht}} = P - T \to T = {F_{ht}} + P$

${{\rm{F}}_{ht}} = P - T \to T = {F_{ht}} + P = m{\omega ^2}r + mg = 0,{4.8^2}.0,5 + 0,4.10 = 16,8N$

Ta có: $\omega  = 2\pi f = 2\pi \dfrac{{360}}{{60}} = 12\pi$

Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm:

Khi trục $\Delta$ quay thì lò xo dãn một đoạn $\Delta l$

$\to {F_{ht}} = {F_{dh}} \leftrightarrow m{\omega ^2}({l_0} + \Delta l) = k\Delta l$

$\to \Delta l(k - m{\omega ^2}) = m{\omega ^2}{l_0}$

$\to \Delta l = \dfrac{{m{\omega ^2}{l_0}}}{{k - m{\omega ^2}}} = \dfrac{{0,01.{{(12\pi )}^2}0,4}}{{125 - 0,01.{{(12\pi )}^2}}} =0,0513m= 5,13cm$

Khối lượng của Trái Đất và vệ tinh lần lượt là M và m.

Bán kính của Trái Đất là R = 6400km. 

Vệ tinh nhân tạo bay quanh Trái Đất ở độ cao h = R

→ Khoảng cách từ vệ tinh đến tâm Trái Đất là: $r = R + h = R + R = 2R$

Khi vệ tinh chuyển động tròn đều quanh Trái Đất, lực hấp dẫn của Trái Đất tác dụng lên vệ tinh đóng vai trò là lực hướng tâm. Ta có:

${F_{hd}} = {F_{ht}} \Leftrightarrow \dfrac{{GmM}}{{{{\left( {R + h} \right)}^2}}} = \dfrac{{m{v^2}}}{{\left( {R + h} \right)}} \Rightarrow v = \sqrt {\dfrac{{GM}}{{R + h}}}  = \sqrt {\dfrac{{GM}}{{2R}}} \,\,\,\left( 2 \right)$

Mặt khác: $g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}\,\,\,\left( 2 \right)$

Thay (2) vào (1) ta có: $v = \sqrt {\dfrac{{g{R^2}}}{{2R}}}  = \sqrt {\dfrac{{gR}}{2}} \, = \sqrt {\dfrac{{{{10.6400.10}^3}}}{2}}  = 5656,9m/s$

Ta có: $v = \omega r = \dfrac{{2\pi }}{T}.\left( {R + h} \right) \Rightarrow T = \dfrac{{2\pi .\left( {R + R} \right)}}{v} = \dfrac{{4\pi .R}}{v} = \dfrac{{4\pi {{.6400.10}^3}}}{{5656,9}} = 14217s$

Có : $\left\{ \begin{array}{l}v = 50m/s\\R = 500m\\m = 1500kg\end{array} \right. \Rightarrow {F_{ht}} = \dfrac{{m{v^2}}}{R} = \dfrac{{{{1500.50}^2}}}{{500}} = 7500N$

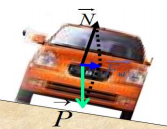
Tại những khúc cua, các tay đua phải thực hiện động tác kỹ thuật nghiêng xe để tạo ra lực hướng tâm giữ cho xe chuyển động trên một cung tròn. Lực hướng tâm trong trường hợp này chính là hợp lực giữa trọng lực, lực ma sát và phản lực.

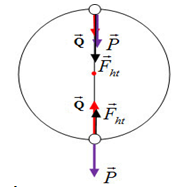
Để không bị rơi xuống thì $N \ge 0$ (lực ép)

Xét chuyển động của diễn viên tại điểm cao nhất ta có:

$\overrightarrow P  + \overrightarrow Q  = \overrightarrow {{F_{ht}}} \,\,\,\left( * \right)$

Chiếu (*) theo phương bán kính hướng vào tâm ta được:

$P + Q = {F_{ht}} \Rightarrow Q = {F_{ht}} - P = \dfrac{{m{v^2}}}{R} - mg$

Mà $N = Q \Rightarrow N = \dfrac{{m{v^2}}}{R} - mg$

Để người không rơi khỏi vòng xiếc tại vị trí cao nhất thì:

$\begin{array}{l}N \ge 0 \Leftrightarrow \dfrac{{m{v^2}}}{R} - mg \ge 0\\ \Rightarrow v \ge \sqrt {gR}  \Leftrightarrow v \ge \sqrt {10.6,4} \\v \ge 8m/s \Rightarrow {v_{\min }} = 8m/s\end{array}$

Các lực tác dụng vào vật :

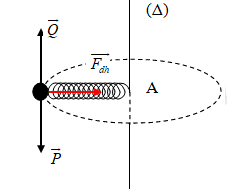
+ Quả cầu chuyển động tròn đều với tốc độ góc $\omega$  quanh trục $\left( \Delta  \right)$

+ Lực đàn hồi lúc này đóng vai trò là lực hướng tâm.

$\Rightarrow {F_{dh}} = {F_{ht}} \Leftrightarrow k.\Delta l = m{\omega ^2}R$

Trong đó :

+ $\Delta l$ là độ dãn của lò xo ;

+ R là bán kính quỹ đạo $\Rightarrow R = l = {l_0} + \Delta l$

Theo bài ra ta có : $\left\{ \begin{array}{l}k = 100N/m\\m = 0,005kg\\R = 0,25 + \Delta l\\\omega  = 20\pi \,\,\left( {rad/s} \right)\end{array} \right.$

 $\begin{array}{l} \Rightarrow 100.\Delta l = 0,005.{\left( {20\pi } \right)^2}.\left( {0,25 + \Delta l} \right)\\ \Leftrightarrow 100.\Delta l = 20.\left( {0,25 + \Delta l} \right) \Leftrightarrow 100.\Delta l = 5 + 20.\Delta l\\ \Leftrightarrow 80.\Delta l = 5 \Rightarrow \Delta l = 0,0625m = 6,25cm\end{array}$

Ta có: $\left\{ \begin{array}{l}m = 0,4kg\\r = 0,5m\\\omega  = 8rad/s\\g = 10m/{s^2}\end{array} \right.$

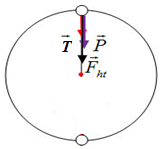
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm.

Ta có: $\overrightarrow {{F_{ht}}}  = \overrightarrow P  + \overrightarrow T \,\,$

Do $\overrightarrow P \,\, \uparrow  \uparrow \,\,\overrightarrow T  \Rightarrow {F_{ht}} = P + T \Rightarrow T = {F_{ht}} - P$

$\Rightarrow T = m{\omega ^2}r-mg = 0,{4.8^2}.0,5 - 0,4.10 = 8,8N$

Ta có lực hấp dẫn giữa vệ tinh và trái đất đóng vai trò là lực hướng tâm.

${F_{ht}} = {F_{hd}} \Leftrightarrow \dfrac{{m{v^2}}}{r} = \dfrac{{G.mM}}{{{r^2}}} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}}$

Tỉ số tốc độ của hai vệ tinh là:

$\dfrac{{{v_2}}}{{{v_1}}} = \dfrac{{\sqrt {\dfrac{{GM}}{{{r_2}}}} }}{{\sqrt {\dfrac{{GM}}{{{r_1}}}} }} = \sqrt {\dfrac{{{r_1}}}{{{r_2}}}}  = \sqrt {\dfrac{r}{{2r}}}  = \dfrac{1}{{\sqrt 2 }} \Rightarrow {v_2} = \dfrac{{{v_1}}}{{\sqrt 2 }}$