Lực ma sát

Ta có, lực ma sát lăn có chiều ngược chiều với ngoại lực hay chính là ngược chiều với vận tốc của vật.

Tủ lạnh trượt thẳng đều trên nền nhà: $F = {F_{m{\rm{s}}}}$

$\to F = \mu N = \mu mg = 0,5.90.10 = 450N$

Ta có: Khi các lực tác dụng lên vật cân bằng nhau thì vật chuyển động thẳng đều.

$\to {F_{m{\rm{s}}}} = F = 30N$

Lực ma sát tác dụng vào thùng là:

$\to {F_{m{\rm{s}}}} = \mu N = \mu mg = 0,35.50.10 = 175N$

Nhận thấy Lực ma sát tác dụng vào thùng lớn hơn lực đẩy của người đẩy thùng nên thùng không chuyển động.

Lực ma sát tác dụng lên vật là: ${F_{m{\rm{s}}}} = \mu N = \mu mg = 0,1.m.10 = mN$

Sử dụng định luật II - Niutơn: $\overrightarrow F  = m\overrightarrow a$ :

${F_{m{\rm{s}}}} = F \leftrightarrow ma = m(N)$

$\to a = 1m/{s^2}$

Ta có:

${v^2} - v_0^2 = 2a{\rm{s}}$

=>$s = \dfrac{{{v_0}^2}}{{2{\rm{a}}}} = \dfrac{{{{10}^2}}}{2} = 50m$

Ta có: $v = {v_0} + at$

Gia tốc của xe là: $a = \dfrac{{ - {v_0}}}{t} = \dfrac{{ - 15}}{{10}} =  - 1,5m/{s^2}$

Khối lượng của xe là: $m = \dfrac{F}{a} = \dfrac{{3000}}{{1,5}} = 2000kg$

Kết quả ở câu a không thay đổi vì khi đó gia tốc không phụ thuộc vào khối lượng( $a = \mu g$ ), kết quả ở câu b có thay đổi vì lực tác dụng có phụ thuộc vào khối lượng ($F = \mu mg$).

Trong điều kiện trên lực tác dụng lên tờ giấy là :

$F = \mu mg = 0,2.0,05.10 = 0,1N$

Để ly bắt đầu trượt trên tờ giấy thì  lực ma sát cân bằng với lực tác dụng vào vật:

${F_{m{\rm{s}}}} = F \leftrightarrow \mu mg = ma$

$\to a = \mu g = 0,3.10 = 3m/{s^2}$

Để ly bắt đầu trượt trên tờ giấy thì  lực ma sát cân bằng với lực tác dụng vào vật:

${F_{m{\rm{s}}}} = F \leftrightarrow \mu mg = ma$

$\to a = \mu g = 0,3.10 = 3m/{s^2}$

+ Khi vật trượt trên đường nằm ngang, có 3 lực tác dụng lên vật: $\overrightarrow P$; $\overrightarrow Q$, ${\overrightarrow F _{mst}}$, $\overrightarrow F$

Theo định luật II Niutơn:

$\overrightarrow F  + \overrightarrow P  + \overrightarrow Q  + \overrightarrow {{F_{m{\rm{s}}}}}  = m\overrightarrow a$

Mà: $\overrightarrow P  + \overrightarrow Q  = \overrightarrow 0$

Nên: $\overrightarrow F  + \overrightarrow {{F_{m{\rm{s}}}}}  = m\overrightarrow a$

+ Chọn chiều dương là chiều chuyển động của vật

$F - {F_{m{\rm{s}}}} = ma$

$\to F = ma + {F_{m{\rm{s}}}}$

Trong đó:

${F_{m{\rm{s}}}} = \mu mg = 0,05.100.9,8 = 49N$

Ta có: ${v^2} - {v_0}^2 = 2{\rm{as}}$ => ${\rm{a = }}\dfrac{{{v^2}}}{{2{\rm{s}}}} = \dfrac{{{{10}^2}}}{{2.100}} = 0,5m/{s^2}$

$\to ma = 100.0,5 = 50N$

Vậy $F = 49 + 50 = 99N$

Vật chuyển động trên mặt phẳng ngang nên:

$P = N = mg$

Độ lớn lực ma sát trượt:

${F_{mst}} = {\mu _t}N = {\mu _t}mg = 0,2.12.10 = 24N$

- Các lực tác dụng lên vật: Lực kéo $\vec F$, lực ma sát ${\vec F_{ms}}$, trọng lực $\vec P$, phản lực $\vec N$

- Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên.

- Phương trình định luật II Niu-tơn dưới dạng véc tơ:

$\vec F + {\vec F_{ms}} + \vec P + \vec N = m.\vec a\,\,\,\left( * \right)$   

- Chiếu (*) lên trục Ox ta được:

$F - {F_{ms}} = ma \Leftrightarrow {F_{ms}} = F - ma$

- Các lực tác dụng lên vật: Lực kéo $\vec F = {\vec F_1} + {\vec F_2}$, lực ma sát ${\vec F_{ms}}$, trọng lực $\vec P$, phản lực $\vec N$

- Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên.

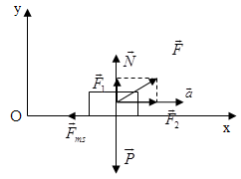
- Phương trình định luật II Niu-tơn dưới dạng véc tơ:

$\vec F + \overrightarrow {{F_{ms}}}  + \vec P + \vec N = m\vec a$    (1)

- Chiếu (1) lên Ox và Oy ta được :

$\left\{ {\begin{array}{*{20}{l}}{{F_2} - {F_{ms}}\; = ma}\\{{F_1} + N - P = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{F.\cos \alpha \; - {F_{ms}} = ma\;\;\;\;\left( 2 \right)}\\{N = P - F\sin \alpha {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 3 \right)}\end{array}} \right.$

Lực ma sát:

${F_{ms}} = {\mu _t}N = {\mu _t}\left( {P - F\sin \alpha } \right) = {\mkern 1mu} {\mu _t}\left( {mg - F\sin \alpha } \right){\mkern 1mu} {\mkern 1mu} \left( 4 \right)$

Từ (2), (3) và (4) ta có :

$\begin{array}{l}ma = F.\cos \alpha  - {\mu _t}\left( {mg - F\sin \alpha } \right)\\ \Rightarrow a = \dfrac{F}{m}\left( {\cos \alpha  + {\mu _t}\sin \alpha } \right) - {\mu _t}g\end{array}$

Thay số ta được:

$a = \dfrac{5}{2}\left( {\cos 30 + 0,2.\sin 30} \right) - 0,2.10 = 0,42m/{s^2}$

Ta có: $\left\{ \begin{array}{l}m = 2T = 1000kg\\{v_0} = 0\\v = 54km/h = 15m/s\\t = 10s\\\mu  = 0,05\end{array} \right.$

Gia tốc của xe: $a = \dfrac{{v - {v_0}}}{t} = \dfrac{{15 - 0}}{{10}} = 1,5m/{s^2}$

Áp dụng định luật II Newton:

$\overrightarrow {F_{ms}} + \overrightarrow P + \overrightarrow N + \overrightarrow F = m.\overrightarrow a\,\,\,\left ( * \right )$

Chiếu (*) trên lên chiều dương ta có:

$\begin{array}{l} - {F_{ms}} + F = ma \Rightarrow F = {F_{ms}} + ma\\ \Leftrightarrow F = \mu mg + ma = m.\left( {\mu g + a} \right)\\ \Leftrightarrow F = 2000.\left( {0,05.10 + 1,5} \right) = 4000N\end{array}$

Chọn chiều dương là chiều chuyển động của xe điện.

Ta có:  ${v_0} = 36km/h = 10m/s$

Kể từ lúc hãm xe, lực ma sát đóng vai trò cản trở chuyển động khiến xe dừng lại.

Áp dụng định luật II Newton, ta có:

$\overrightarrow {F_{ms}} + \overrightarrow P + \overrightarrow N + \overrightarrow F = m.\overrightarrow a\,\,\,\left ( * \right )$

Chiếu (*) lên chiều chuyển động ta có:

$\begin{array}{l} - {F_{ms}} = ma \Leftrightarrow  - \mu mg = ma\\ \Rightarrow a =  - \mu g =  - 0,2.9,8 =  - 1,96m/{s^2}\end{array}$ 

Quãng đường vật đi được kể từ lúc hãm phanh đến khi dừng hẳn:

${v^2} - v_0^2 = 2as \Rightarrow s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{{0^2} - {{10}^2}}}{{2.\left( { - 1,96} \right)}} = 25,51m$

Chọn chiều dương là chiều chuyển động của quả bóng.

Áp dụng định luật II Niuton ta có: $\overrightarrow {{F_{ms}}}  + \overrightarrow N  + \overrightarrow P  = m.\vec a{\mkern 1mu} {\mkern 1mu} \,\,\left( * \right)$

Chiếu (*) lên phương chuyển động ta có :

$\begin{array}{*{20}{l}}{{F_{ms}} = m.a \Leftrightarrow  - \mu N = ma \Rightarrow  - \mu mg = ma}\\{ \Rightarrow a =  - \mu g =  - 0,15.10 =  - 1,5m/{s^2}}\end{array}$

Ta có : $\left\{ {\begin{array}{*{20}{l}}{{v_0} = 15m/s}\\{v = 0}\\{a =  - 1,5m/{s^2}}\end{array}} \right.$

Áp dụng công thức liên hệ giữa gia tốc, vận tốc và quãng đường ta có :

${v^2} - v_0^2 = 2as \Rightarrow s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{{0^2} - {{15}^2}}}{{2.\left( { - 1,5} \right)}} = 75m$

Xe chuyển động thẳng đều $\Rightarrow$ lực ma sát cân bằng với lực tác dụng.

+ Khi chưa chất hàng lên:

$F_{ms} = F \Leftrightarrow \mu mg = F\,\,\,\left ( 1 \right )$

+ Khi chất thêm hàng:

$F_{ms}' = F' \Leftrightarrow \mu \left ( m + 20 \right )g = F'\,\,\,\left ( 2 \right )$

Lấy $\dfrac{{\left( 1 \right)}}{{\left( 2 \right)}} \Rightarrow \dfrac{m}{{m + 20}} = \dfrac{{20}}{{60}} = \dfrac{1}{3}$

$\Leftrightarrow 3m = m + 20 \Rightarrow m = 10kg$

Thay vào (1) ta được: $\mu .10.10. = 20 \Rightarrow \mu  = 0,2$

Lực làm cản trở chuyển động của xe trên mặt đường là lực ma sát:

${F_{ms}} = \mu .N = \mu mg = 0,08.1500.9,8 = 1176N$

Khi lực ép (áp lực) lên mặt tiếp xúc tăng thì lực ma sát tăng.

Còn hệ số ma sát chỉ phụ thuộc vào tính chất của mặt tiếp xúc (vật liệu, tình trạng mặt tiếp xúc) nên nếu lực ép hai mặt tiếp xúc tăng lên thì hệ số ma sát giữa hai mặt đó không thay đổi.