Tìm tất cả các giá trị thực của tham số $m$ sao cho hàm số $y = \dfrac{{mx + 4}}{{x + m}}$ nghịch biến trên khoảng $\left( { - {\mkern 1mu} \infty ;1} \right).$
Ta có $y = \dfrac{{mx + 4}}{{x + m}} \Rightarrow y' = \dfrac{{{m^2} - 4}}{{{{\left( {x + m} \right)}^2}}};{\mkern 1mu} {\mkern 1mu} \forall x \ne - {\mkern 1mu} m.$
Yêu cầu bài toán $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y' < 0}\\{x = {\rm{\;}} - m \notin \left( { - \infty ;1} \right)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 4 < 0}\\{ - m \ge 1}\end{array}} \right. \Leftrightarrow {\rm{\;}} - 2 < m \le - 1.$
Với giá trị nào của $m$ thì hàm số $y = \dfrac{{\left( {m + 1} \right)x + 2m + 2}}{{x + m}}$ nghịch biến trong khoảng $\left( { - 1; + \infty {\rm{\;}}} \right)$?
TXĐ: $D = \mathbb{R}\backslash \left\{ { - m} \right\}$.
Ta có $y' = \dfrac{{m\left( {m + 1} \right) - 2m - 2}}{{{{\left( {x + m} \right)}^2}}} = \dfrac{{{m^2} - m - 2}}{{{{\left( {x + m} \right)}^2}}}$.
Để hàm số nghịch biến trên khoảng $\left( { - 1; + \infty {\rm{\;}}} \right)$ thì
$\left\{ {\begin{array}{*{20}{l}}{y' < 0}\\{ - m \notin \left( { - 1; + \infty } \right)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - m - 2 < 0}\\{ - m \le {\rm{\;}} - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 1 < m < 2}\\{m \ge 1}\end{array}} \right. \Leftrightarrow 1 \le m < 2$.
Cho bất phương trình \(\sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^2}\left( {{x^2} - 1} \right) > 1 - m\). Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình nghiệm đúng với mọi \(x > 1.\)
Ta có \(\sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^2}\left( {{x^2} - 1} \right) > 1 - m\)
\( \Leftrightarrow \sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^4} - {x^2} > 1 - m\)
\( \Leftrightarrow \sqrt[3]{{{x^4} + {x^2} + m}} + {x^4} + {x^2} + m > \sqrt[3]{{2{x^2} + 1}} + 2{x^2} + 1\) (*)
Xét hàm số \(f\left( t \right) = {t^3} + t\,\,\, \Rightarrow y' = 2{t^2} + 1 > 0\) nên hàm số \(f\left( t \right)\) là hàm đồng biến
Khi đó phương trình (*) trở thành:
\(f\left( {\sqrt[3]{{{x^4} + {x^2} + m}}} \right) > f\left( {\sqrt[3]{{2{x^2} + 1}}} \right)\) \( \Leftrightarrow \sqrt[3]{{{x^4} + {x^2} + m}} > \sqrt[3]{{2{x^2} + 1}}\) \( \Leftrightarrow {x^4} + {x^2} + m > 2{x^2} + 1\) \( \Leftrightarrow m > {\rm{\;}} - {x^4} + {x^2} + 1\)
Xét hàm số \(g\left( x \right) = - {x^4} + {x^2} + 1\) với \(x > 1\)
Có \(g'\left( x \right) = - 4{x^3} + 2x = - 2x\left( {2{x^2} - 1} \right) < 0;\,\forall x > 1\)
Ta có BBT của hàm \(g\left( x \right) = - {x^4} + {x^2} + 1\) với \(x > 1\)
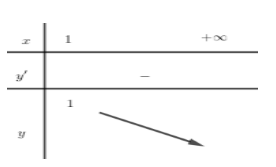
Từ BBT suy ra \(m \ge 1.\)
Trong năm 2018, nhà trường đã dành khoảng bao nhiêu phần trăm tổng lượng chi vào mua sách ?
Năm 2018 có kinh phí dự trù là :
\(2 \times {10^9} - 200 = 18 \times {10^8}\) (đồng)
Số tiền chi cho mua sách năm 2018 là :
\(2 \times {10^9}:100 \times 10 - 38 \times {10^6} = 162 \times {10^6}\) (đồng)
Số tiền chi cho mua sách năm 2018 chiếm số phần trăm tổng kinh phí dự trù của năm đó là :
\(162 \times {10^6}:\left( {18 \times {{10}^8}} \right) \times 100 = 9\% \)
Lương chi cho cán bộ quản lí ít hơn lương chi cho giáo viên bao nhiêu phần trăm?
Biểu đồ có lương giáo viên chiếm 45%; lương cán bộ quản lí chiếm 15%.
Lương cán bộ quản lí ít hơn lương chi cho giáo viên theo phân bổ dự trù kinh phí năm là : \(45\% - 15\% = 30\% .\)
Trong năm 2019, trường phổ thông đó phải chi bao nhiêu tiền cho lương cán bộ quản lí ?
Biểu đồ có lương cán bộ quản lí chiếm 15%.
Trong năm 2019, trường phổ thông đó chi số tiền cho lương cán bộ quản lí là :
\(2 \times {10^9}:100 \times 15 = 3 \times {10^8}\) (đồng) hay 300 triệu đồngChọn B.
Đề thi THPT QG - 2021 - mã 102
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Trong khoảng từ \(\left( {0;1} \right)\) đồ thị hàm số đi lên nên \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng:
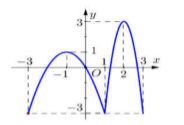
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên các khoảng \(\left( { - 3;\, - 1} \right)\) và \(\left( {1;\,\,2} \right).\)
Hàm số nghịch biến trên các khoảng: \(\left( { - 1;\,1} \right)\) và \(\left( {2;\,\,3} \right).\)
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = - {x^3} - 6{x^2} + \left( {4m - 9} \right)x + 4\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\) là:
Ta có : \(f'\left( x \right) = - 3{x^2} - 12x + \left( {4m - 9} \right)\)
Hàm số đã cho nghịch biến trên \(\left( { - \infty ; - 1} \right) \Leftrightarrow f'\left( x \right) \le 0\,\,\forall x \in \left( { - \infty ; - 1} \right)\)
\(\begin{array}{l} \Leftrightarrow - 3{x^2} - 12x + \left( {4m - 9} \right) \le 0\;\;\forall x \in \left( { - \infty ; - 1} \right)\\ \Leftrightarrow 4m \le 3{x^2} + 12x + 9 = g\left( x \right)\;\;\forall x \in \left( { - \infty ; - 1} \right)\\ \Rightarrow 4m \le \mathop {\min }\limits_{\left( { - \infty ; - 1} \right)} g\left( x \right)\end{array}\)
Xét hàm số :\(g\left( x \right) = 3{x^2} + 12x + 9\) ta có : \(g'\left( x \right) = 6x + 12 = 0 \Leftrightarrow x = - 2\)
\( \Rightarrow \mathop {\min }\limits_{\left( { - \infty ; - 1} \right)} g\left( x \right) = g\left( { - 2} \right) = - 3\)
\( \Rightarrow 4m \le - 3 \Leftrightarrow m \le - \dfrac{3}{4}\)
Cho hàm số \(f(x)\) có đạo hàm \(f'(x) = {(x + 1)^2}{(x - 1)^3}(2 - x)\). Hàm số đồng biến trên khoảng nào dưới đây?
Bước 1: Giải phương trình \(f'\left( x \right) = 0\) tìm nghiệm bội lẻ.
Ta có \(f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 1}\\{x = 2}\end{array}} \right.\)
Vì $x=-1$ là nghiệm bộ 2 của phương trình nên $x=-1$ không là điểm cực trị.
Bước 2: Lập bảng biến thiên và tìm khoảng đồng biến.
Ta có bảng biến thiên:
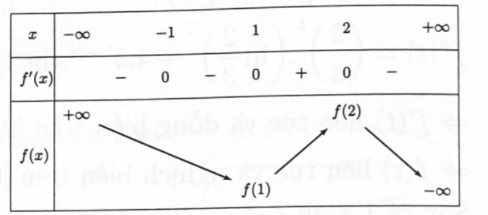
=> Dựa vào bảng biến thiên, ta thấy hàm số đồng biến trên khoảng \((1;2)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:
Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng:
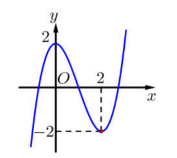
Dựa vào đồ thị hàm số ta có hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng \(\left( { - \infty ;\,0} \right)\) và \(\left( {2;\, + \infty } \right).\)
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {0;\,\,2} \right).\)
Xét hàm số: \(y = - 2f\left( x \right)\) ta có: \(y' = - 2f'\left( x \right).\)
Hàm số đồng biến \( \Leftrightarrow - 2f'\left( x \right) \ge 0 \Leftrightarrow f'\left( x \right) \le 0 \Leftrightarrow 0 \le x \le 2.\)
Vậy hàm số \(y = - 2f\left( x \right)\) đồng biến \( \Leftrightarrow x \in \left[ {0;\,2} \right].\)
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:
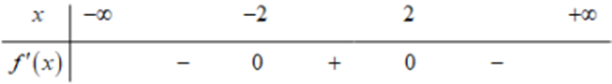
Hàm số đã cho nghịch biến trên khoảng nào dưới đây
Hàm số đã cho nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\).
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị của hàm\(y = f'\left( x \right)\) như hình vẽ. Xét hàm số \(g(x) = f\left( {{x^2} - 2} \right)\). Mệnh đề nào dưới đây sai ?
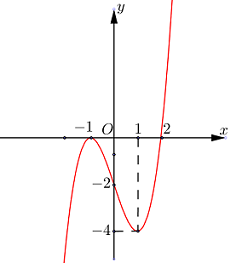
Ta có: \(g'\left( x \right) = 2x\,f'\left( {{x^2} - 2} \right)\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 2 = - 1\\{x^2} - 2 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\\x = \pm 2\end{array} \right.\).
Vì -1 là điểm cực đại của \(f'(x)\) nên \(\pm 1\) là điểm cực đại của \(f'(x^2-2)\). Do đó \(f'(x^2-2)\) không đổi dấu qua \(\pm 1\) và luôn mang dấu dương.
Bảng xét dấu \(g'\left( x \right)\):
![]()
Vậy hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - 1;0} \right)\) là phát biểu sai.
Cho hàm số \(y = {x^3} - 3{x^2} - 2020.\) Mệnh đề nào dưới đây đúng ?
TXĐ: \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2} - 6x,\,\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).
Bảng xét dấu đạo hàm:
![]()
Dựa vào bảng xét dấu ta suy ra hàm số nghịch biến trên khoảng \(\left( {0;2} \right).\)
Cho hàm số \(f\left( x \right)\) có bảng xét dấu có đạo hàm như hình bên dưới
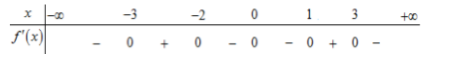
Hàm số \(y = f\left( {1 - 2x} \right)\) đồng biến trên khoảng
Ta có: \(y' = - 2f'\left( {1 - 2x} \right)\).
Với \(x = 1 \Rightarrow y'\left( 1 \right) = - 2f'\left( { - 1} \right) > 0 \Rightarrow \) Loại đáp án B, C, D.
Hàm số \(y = 2{x^3} - 9{x^2} + 12x + 3\) nghịch biến trên những khoảng nào?
Ta có: \(y' = 6{x^2} - 18x + 12\).
\(y' < 0 \Leftrightarrow 6{x^2} - 18x + 12 < 0 \Leftrightarrow 1 < x < 2\).
Vậy hàm số đã cho đồng biến trên \(\left( {1;2} \right)\).
Tập hợp tất cả các giá trị của tham số \(m\) để hàm số \(y = \dfrac{{mx - 4}}{{x - m}}\) đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\) là:
ĐKXĐ: \(x \ne m\).
Ta có: \(y' = \dfrac{{ - {m^2} + 4}}{{{{\left( {x - m} \right)}^2}}}\).
Để hàm số đồng biến trên \(\left( { - 1; + \infty } \right)\) thì \(\left\{ \begin{array}{l}y' > 0\\m \notin \left( { - 1; + \infty } \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - {m^2} + 4 > 0\\m \le - 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - 2 < m < 2\\m \le - 1\end{array} \right. \Leftrightarrow - 2 < m \le - 1\).
Vậy \(m \in \left( { - 2; - 1} \right]\).
Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = {x^3} - 3\left( {2m + 1} \right){x^2} + \left( {12m + 5} \right)x + 2\) đồng biến trên khoảng \(\left( {2; + \infty } \right).\) Số phần tử của \(S\) bằng:
Xét hàm số: \(y = {x^3} - 3\left( {2m + 1} \right){x^2} + \left( {12m + 5} \right) + 2\)
\(\begin{array}{l} \Rightarrow y' = 3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5\\ \Rightarrow y' = 0 \Leftrightarrow 3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5 = 0\,\,\,\,\left( * \right)\end{array}\)
Hàm số đã cho đồng biến trên khoảng \(\left( {2; + \infty } \right).\) khi và chỉ khi \(y' \ge 0\forall x \in \left( {2; + \infty } \right)\)
\(\begin{array}{l} \Leftrightarrow 3{x^2} - 6\left( {2m - 1} \right)x + 12m + 5 \ge 0\forall x \in \left( {2; + \infty } \right)\\ \Leftrightarrow m \le \dfrac{{3{x^2} - 6x + 5}}{{12\left( {x - 1} \right)}}\forall x \in \left( {2; + \infty } \right)\end{array}\)
Xét hàm số \(f\left( x \right) = \dfrac{{3{x^2} - 6x + 5}}{{12\left( {x - 1} \right)}},\forall x \in \left( {2; + \infty } \right)\)
Ta có: \(f'\left( x \right) = \dfrac{{3{x^2} - 6x + 1}}{{12{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in \left( {2; + \infty } \right)\)
\( \Rightarrow \)Hàm số \(f'\left( x \right)\) đồng biến trong khoảng \(\left( {2; + \infty } \right)\)
Do đó \(m \le f\left( x \right),\forall x \in \left( {2; + \infty } \right)\)\( \Rightarrow m \le f\left( 2 \right) \Leftrightarrow m \le \dfrac{5}{{12}}\)
Vì \(0 < m \le \dfrac{5}{{12}}\)
Do đó không có giá trị nguyên dương nào của m thỏa mãn bài toán.
Hàm số nào dưới đây nghịch biến trên \(\mathbb{R}\)?
Loại đáp án A và B vì hàm bậc bốn trùng phương và hàm phân thức bậc nhất trên bậc nhất không thể nghịch biến trên \(\mathbb{R}\).
Loại đáp án D vì hàm đa thức bậc ba với hệ số của \({x^3}\) dương không thể nghịch biến trên \(\mathbb{R}\).
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu \(f'\left( x \right)\) như sau:
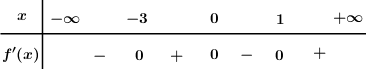
Hàm số \(y = f\left( {2 - 3x} \right)\) đồng biến trên khoảng nào sau đây?
Đặt \(g\left( x \right) = f\left( {2 - 3x} \right)\) ta có: \(g'\left( x \right) = - 3f'\left( {2 - 3x} \right)\).
Xét \(g'\left( x \right) > 0 \Leftrightarrow - 3f'\left( {2 - 3x} \right) > 0\) \( \Leftrightarrow f'\left( {2 - 3x} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}2 - 3x < - 3\\0 < 2 - 3x < 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x > \dfrac{5}{3}\\1 < 3x < 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > \dfrac{5}{3}\\\dfrac{1}{3} < x < \dfrac{2}{3}\end{array} \right.\).
Suy ra hàm số \(y = f\left( {2 - 3x} \right)\) đồng biến trên \(\left( {\dfrac{5}{3}; + \infty } \right)\) và \(\left( {\dfrac{1}{3};\dfrac{2}{3}} \right)\).
Dựa vào các đáp án ta thấy hàm số đồng biến trên \(\left( {2;3} \right)\).

