Câu hỏi:
2 năm trước
Cho hàm số \(f\left( x \right)\) có bảng xét dấu có đạo hàm như hình bên dưới
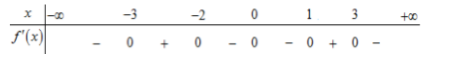
Hàm số \(y = f\left( {1 - 2x} \right)\) đồng biến trên khoảng
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có: \(y' = - 2f'\left( {1 - 2x} \right)\).
Với \(x = 1 \Rightarrow y'\left( 1 \right) = - 2f'\left( { - 1} \right) > 0 \Rightarrow \) Loại đáp án B, C, D.
Hướng dẫn giải:
Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {a;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right)\) và bằng 0 tại hữu hạn điểm.
Giải thích thêm:
Ngoài phương pháp thử HS có thể lập BXD \(y'\), tuy nhiên trong bài tập này, thử là phương pháp tối ưu nhất.
Cách tự luận:
\(\begin{array}{l}y' > 0 \Leftrightarrow - 2f'\left( {1 - 2x} \right) > 0\\ \Leftrightarrow f'\left( {1 - 2x} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}1 - 2x < - 3\\ - 2 < 1 - 2x < 0\\0 < 1 - 2x < 1\\1 - 2x > 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\frac{1}{2} < x < \frac{3}{2}\\0 < x < \frac{1}{2}\\x < - 1\end{array} \right.\end{array}\)
Nên hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right),\left( {0;\frac{3}{2}} \right),\left( {2; + \infty } \right)\)
(trong khoảng \(\left( {0;\frac{3}{2}} \right)\) chứa điểm \(x = \frac{1}{2}\) làm cho đạo hàm \(f'\left( {1 - 2x} \right) = 0\) vẫn được)
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
