Câu hỏi:
2 năm trước
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu \(f'\left( x \right)\) như sau:
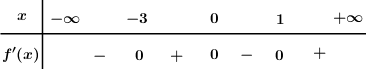
Hàm số \(y = f\left( {2 - 3x} \right)\) đồng biến trên khoảng nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: c
Đặt \(g\left( x \right) = f\left( {2 - 3x} \right)\) ta có: \(g'\left( x \right) = - 3f'\left( {2 - 3x} \right)\).
Xét \(g'\left( x \right) > 0 \Leftrightarrow - 3f'\left( {2 - 3x} \right) > 0\) \( \Leftrightarrow f'\left( {2 - 3x} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}2 - 3x < - 3\\0 < 2 - 3x < 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x > \dfrac{5}{3}\\1 < 3x < 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > \dfrac{5}{3}\\\dfrac{1}{3} < x < \dfrac{2}{3}\end{array} \right.\).
Suy ra hàm số \(y = f\left( {2 - 3x} \right)\) đồng biến trên \(\left( {\dfrac{5}{3}; + \infty } \right)\) và \(\left( {\dfrac{1}{3};\dfrac{2}{3}} \right)\).
Dựa vào các đáp án ta thấy hàm số đồng biến trên \(\left( {2;3} \right)\).
Hướng dẫn giải:
- Đặt \(g\left( x \right) = f\left( {2 - 3x} \right)\), tính đạo hàm của hàm số.
- Giải bất phương trình \(g'\left( x \right) > 0\).
- Dựa vào các đáp án xác định khoảng đồng biến của hàm số.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
