Câu hỏi:
2 năm trước
Cho hàm số \(f(x)\) có đạo hàm \(f'(x) = {(x + 1)^2}{(x - 1)^3}(2 - x)\). Hàm số đồng biến trên khoảng nào dưới đây?
Trả lời bởi giáo viên
Đáp án đúng: b
Bước 1: Giải phương trình \(f'\left( x \right) = 0\) tìm nghiệm bội lẻ.
Ta có \(f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 1}\\{x = 2}\end{array}} \right.\)
Vì $x=-1$ là nghiệm bộ 2 của phương trình nên $x=-1$ không là điểm cực trị.
Bước 2: Lập bảng biến thiên và tìm khoảng đồng biến.
Ta có bảng biến thiên:
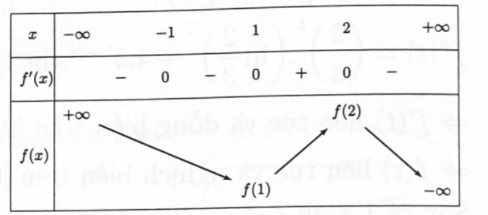
=> Dựa vào bảng biến thiên, ta thấy hàm số đồng biến trên khoảng \((1;2)\).
Hướng dẫn giải:
Bước 1: Giải phương trình \(f'\left( x \right) = 0\) tìm nghiệm bội lẻ.
Bước 2: Lập bảng biến thiên và tìm khoảng đồng biến.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
