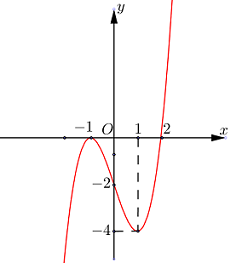
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị của hàm\(y = f'\left( x \right)\) như hình vẽ. Xét hàm số \(g(x) = f\left( {{x^2} - 2} \right)\). Mệnh đề nào dưới đây sai ?

Giải thích thêm:

Có thể xét dấu bằng 2 cách như sau:

Cách 1:

\(\begin{array}{l}g'\left( x \right) \ge 0 \Leftrightarrow 2xf'\left( {{x^2} - 2} \right) \ge 0\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 0\\f'\left( {{x^2} - 2} \right) \ge 0\end{array} \right.\\\left\{ \begin{array}{l}x \le 0\\f'\left( {{x^2} - 2} \right) \le 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 0\\{x^2} - 2 \ge 2\end{array} \right.\\\left\{ \begin{array}{l}x \le 0\\{x^2} - 2 \le 2\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 0\\{x^2} \ge 4\end{array} \right.\\\left\{ \begin{array}{l}x \le 0\\{x^2} \le 4\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 0\\\left[ \begin{array}{l}x \ge 2\\x \le  - 2\end{array} \right.\end{array} \right.\\\left\{ \begin{array}{l}x \le 0\\ - 2 \le x \le 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\ - 2 \le x \le 0\end{array} \right.\end{array}\)

Do đó

\(g'\left( x \right) \le 0 \Leftrightarrow \left[ \begin{array}{l}x \le  - 2\\0 \le x \le 2\end{array} \right.\).

Cách 2:

Xét trong khoảng \(\left( {2; + \infty } \right)\), chọn \(x = 3\) ta được:

\(g'\left( 3 \right) = 2.3.f'\left( {{3^2} - 2} \right) = 6f'\left( 7 \right)\)

Quan sát đồ thị hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( 7 \right) > 0\) nên \(g'\left( 3 \right) > 0\).

Do đó ta điền dấu \( + \) vào khoảng \(\left( {2; + \infty } \right)\).

Qua nghiệm \(x = 2\) (nghiệm đơn) nên đạo hàm đổi dấu, ta điền dấu \( - \)

Qua nghiệm \(x = 1\) (bội chẵn) nên đạo hàm không đổi dấu, ta điền tiếp dấu \( - \)

Qua nghiệm \(x = 0\) (nghiệm đơn) nên đạo hàm đổi dấu, ta điền dấu \( + \)

Qua nghiệm \(x =  - 1\) (bội chẵn) nên đạo hàm không đổi dấu, ta điền tiếp dấu \( + \)

Qua nghiệm \(x =  - 2\) (nghiệm đơn) nên đạo hàm đổi dấu, ta điền dấu \( - \)