Bài tập ôn tập chương 4

Ta có: $z = {\left( {\sqrt 2  + 3i} \right)^2} = 2 + 6\sqrt 2 i + 9{i^2} =  - 7 + 6\sqrt 2 i$

Ta có: ${\left( {1 + i} \right)^2}\left( {2 - i} \right)z = 8 + i + \left( {1 + 2i} \right)z$

$\begin{array}{l} \Leftrightarrow \left( {1 + 2i + {i^2}} \right)\left( {2 - i} \right)z = 8 + i + \left( {1 + 2i} \right)z\\ \Leftrightarrow \left( {2 + 4i} \right)z = 8 + i + \left( {1 + 2i} \right)z\\ \Leftrightarrow \left( {1 + 2i} \right)z = 8 + i\end{array}$

$\Rightarrow$ $z = \dfrac{{8 + i}}{{1 + 2i}} = \dfrac{{\left( {8 + i} \right)\left( {1 - 2i} \right)}}{{\left( {1 + 2i} \right)\left( {1 - 2i} \right)}}$ $= \dfrac{{10 - 15i}}{{{1^2} + {2^2}}} = 2 - 3i$

Phần thực của số phức $z$ là $2$.

Giả sử $z  = a + bi (a, b \in R)$ $\Rightarrow$ $\overline z  = a - bi$

Ta có: $z + \overline z  = a + bi + a - bi = 2a$ là một số thực $\Rightarrow$ A đúng

$z - \overline z  = a + bi - a + bi = 2bi$ là một số ảo $\Rightarrow$ B đúng

$z.\overline z  = (a + bi).(a - bi) = {a^2} + {b^2}$ là một số thực $\Rightarrow$ C đúng

${z^2} + {\overline z ^2} = {(a + bi)^2} + {(a - bi)^2} = 2{a^2} - 2{b^2}$ là một số thực $\Rightarrow$ D sai

Ta có: ${z_1} = 1 + 2i;$${z_2} = 2 - 3i$$\Rightarrow 3{z_1}--2{z_2} = 3\left( {1 + 2i} \right) - 2\left( {2 - 3i} \right)$ $= 3 + 6i - 4 + 6i =  - 1 + 12i$

Vậy phần ảo của số phức đó là $12$.

Điểm biểu diễn của số phức z là $M(1;2) \Rightarrow z = 1 + 2i$

${\rm{w}} = z - 2\overline z  = \left( {1 + 2i} \right) - 2\left( {1 - 2i} \right) =  - 1 + 6i$

$\Rightarrow$ Điểm biểu diễn của số phức ${\rm{w}} = z - 2\overline z$ là $(-1; 6).$

${z^2} - 4z + 5 = 0 \Leftrightarrow {z_{1,2}} = 2 \pm i \Rightarrow {\left| {{z_1}} \right|^2} = {\left| {{z_2}} \right|^2} = {2^2} + {1^2} = 5$

$\begin{array}{l}P = \left( {{z_1} - 2{z_2}} \right).\overline {{z_2}}  - 4{z_1}\\P = \left( {2 + i - 2\left( {2 - i} \right)} \right).\left( {2 + i} \right) - 4\left( {2 + i} \right)\\P = \left( { - 2 + 3i} \right)\left( {2 + i} \right) - 4\left( {2 + i} \right)\\P =  - 7 + 4i - 8 - 4i =  - 15\end{array}$

Số phức liên hợp của số phức $z = 3 + 2i$ là $\overline z  = 3 - 2i$.

Giả sử $z = x + yi,\,\,\left( {x,y \in R} \right)$

Theo đề bài ta có: $\left| {z + 3 - 4i} \right| = 5 \Leftrightarrow \sqrt {{{(x + 3)}^2} + {{(y - 4)}^2}}  = 5 \Leftrightarrow {(x + 3)^2} + {(y - 4)^2} = 25$

Vậy, tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là đường tròn tâm $I( - 3;4),\,R = 5$.

Đặt $z = a + bi,\,\left( {a,b \in R} \right)$.

$\begin{array}{l}iz + (1 - i)\overline z  =  - 2i \Leftrightarrow i(a + bi) + (1 - i)(a - bi) =  - 2i \Leftrightarrow ai - b + a - bi - ai - b =  - 2i\\ \Leftrightarrow  - bi + a - 2b =  - 2i \Leftrightarrow \left\{ \begin{array}{l} - b =  - 2\\a - 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2\\a = 4\end{array} \right. \Rightarrow a + b = 6\end{array}$

Tổng của phần thực và phần ảo là 6.

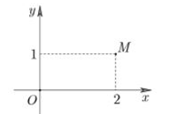
Ta có $M\left( {2;\;1} \right)$ biểu diễn số phức $z \Rightarrow z = 2 + i \Rightarrow \overline z  = 2 - i.$

+) Xét phương trình: ${z^2} - 2z + 3 = 0 \Leftrightarrow {z^2} - 2z + 1 + 2 = 0 \Leftrightarrow {\left( {z - 1} \right)^2} =  - 2 \Leftrightarrow {\left( {z - 1} \right)^2} = 2{i^2}$

$\Leftrightarrow \left| {z - 1} \right| = \sqrt 2 i \Leftrightarrow \left[ \begin{array}{l}z - 1 = \sqrt 2 i\\z - 1 =  - \sqrt 2 i\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = 1 + \sqrt 2 i\\z = 1 - \sqrt 2 i\end{array} \right. \Rightarrow$ loại đáp án A.

+) Xét phương trình: ${z^2} + 2z + 5 = 0 \Leftrightarrow {z^2} + 2z + 4 + 1 = 0 \Leftrightarrow {\left( {z + 2} \right)^2} =  - 1 = {i^2}$

$\Leftrightarrow \left| {z + 2} \right| = i \Leftrightarrow \left[ \begin{array}{l}z + 2 = i\\z + 2 =  - i\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z =  - 2 + i\\z =  - 2 - i\end{array} \right. \Rightarrow$ loại đáp án B.

+) Xét phương trình: ${z^2} - 2z + 5 = 0 \Leftrightarrow {z^2} - 2z + 1 + 4 = 0 \Leftrightarrow {\left( {z - 1} \right)^2} =  - 4 =  - 4{i^2}$

$\Leftrightarrow \left| {z - 1} \right| = 2i \Leftrightarrow \left[ \begin{array}{l}z - 1 = 2i\\z - 1 =  - 2i\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = 1 + 2i\\z = 1 - 2i\end{array} \right. \Rightarrow$ chọn đáp án C.

Đặt $z = a + bi\,\,\left( {a;b \in R} \right) \Rightarrow \overline z  = a - bi$, khi đó ta có:

$\begin{array}{l}\,\,\,\,\left( {1 + i} \right)\left( {a + bi} \right) + \left( {2 - i} \right)\left( {a - bi} \right) = 13 + 2i\\ \Leftrightarrow a - b + \left( {a + b} \right)i + 2a - b - \left( {a + 2b} \right)i = 13 + 2i\\ \Leftrightarrow 3a - 2b - bi = 13 + 2i\\ \Leftrightarrow \left\{ \begin{array}{l}3a - 2b = 13\\ - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b =  - 2\end{array} \right. \Rightarrow z = 3 - 2i\end{array}$

Ta có $z\left( {1 + i} \right) = 3 - 5i \Leftrightarrow z = \dfrac{{3 - 5i}}{{1 + i}} = \dfrac{{\left( {3 - 5i} \right)\left( {1 - i} \right)}}{{1 - {i^2}}} =  - 1 - 4i \Rightarrow \left| z \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 4} \right)}^2}}  = \sqrt {17} .$

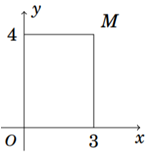
Từ hình vẽ, ta có $M\left( {3;4} \right)$ nên $z = 3 + 4i$. Vậy phần thực bằng $3$ và phần ảo bằng $4$.

Phương trình: $8{z^2} - 4z + 1 = 0$

Có: $\Delta ' = 4 - 8 =  - 4 = 4{i^2}$

 $\Rightarrow$ Phương trình có $2$  nghiệm là: ${z_1} = \dfrac{{2 + 2i}}{8} = \dfrac{1}{4} + \dfrac{1}{4}i;{z_2} = \dfrac{{2 - 2i}}{8} = \dfrac{1}{4} - \dfrac{1}{4}i$

Ta có: ${z_1} + {z_2} = \dfrac{{ - 1 - 5i\sqrt 5 }}{3} + \dfrac{{ - 1 + 5i\sqrt 5 }}{3} = \dfrac{{ - 2}}{3}$

           ${z_1}.{z_2} = \dfrac{{ - 1 - 5i\sqrt 5 }}{3}.\dfrac{{ - 1 + 5i\sqrt 5 }}{3} = \dfrac{{126}}{9} = \dfrac{{42}}{3}$

$\Rightarrow {z_1};{z_2}$ là các nghiệm của phương trình: ${z^2} + \dfrac{2}{3}z + \dfrac{{42}}{3} = 0 \Leftrightarrow 3{z^2} + 2z + 42 = 0$

) Sai vì nếu $\Delta  < 0$ thì $\sqrt \Delta   =  \pm i\sqrt {\left| \Delta  \right|}$ do đó phương trình có $2$  nghiệm phức

2) Đúng

3) Đúng

Vậy có $2$  mệnh đề đúng

Phương trình: ${z^2}-2z + 5 = 0$

Có: $\Delta ' = 1 - 5 =  - 4 = 4{i^2}$

   $\Rightarrow \sqrt {\Delta '}  = \sqrt {4{i^2}}  = 2i$

$\Rightarrow$ Phương trình có $2$  nghiệm là: ${z_1} = 1 + 2i;{z_2} = 1 - 2i$

Khi đó: $A\left( {1;2} \right),B(1; - 2)$

Tọa độ trung điểm đoạn thẳng $AB$ là: $\left( {1;0} \right)$

Giả sử số phức cần tìm là $z = a + bi$.

Từ điều kiện $z = \bar z$ ta có $a + bi = a - bi \Leftrightarrow b = 0$

Từ điều kiện $|z| = 5 \Rightarrow a =  \pm 5$

Vì $z$ là thuần ảo nên $a = 0 \Rightarrow z = bi$. Từ điều kiện $|z + 4| = 3|z|$ có

$\left| {bi + 4} \right| = 3\left| {bi} \right| \Leftrightarrow {b^2} + {4^2} = 9{b^2} \Leftrightarrow 8{b^2} = 16 \Leftrightarrow {b^2} = 2 \Leftrightarrow b =  \pm \sqrt 2$

Mỗi một số phức $z$ chỉ có $1$  điểm biểu diễn trên mặt phẳng phức.