CHỨNG MINH BA ĐƯỜNG THẲNG ĐỒNG QUY
A. Phương pháp giải
+ Chứng minh một điểm đồng thời thuộc cả ba đường thẳng đó
+ Chứng minh giao điểm của hai đường thẳng này nằm trên đường thẳng thứ ba
+ Chứng minh giao điểm của hai đường thẳng thứ nhất và thứ hai trùng với giao điểm của hai đường thẳng thứ hai và thứ b
+ Sử dụng tính chất đồng quy của ba đường trung tuyến, đường cao, phân giác, trung trực trong tam giác
+ Sử dụng tính chất của đường chéo của các tứ giác đặc biệt
B. Ví dụ minh họa
Ví dụ 1. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Các đường thẳng AO và AO’ cắt (O) tại C và D và cắt (O’) tại E và F. Chứng minh rằng AB, CD, EF đồng quy.
Hướng dẫn giải
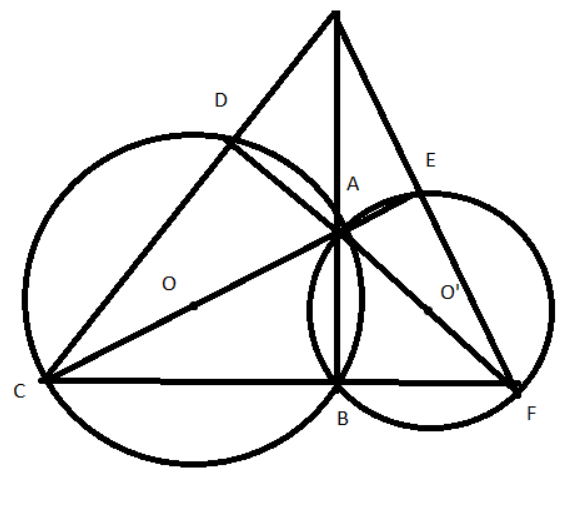
+ Có nhìn đường kính AC nên
+ Có nhìn đường kính AF nên
+ Có nhìn đường kính AC nên
+ Có nhìn đường kính AF nên
+ Có
Suy ra 3 điểm E, B, F thẳng hàng
+ Xét tam giác CAF có các đường cao là AB, CD, EF nên AB, CD, EF đồng quy.
Ví dụ 2. Cho tam giác đều ABC nội tiếp đường tròn đường kính AD. Gọi M là một điểm di động trên cung nhỏ AB (M không trùng với các điểm A và B). Gọi K là giao điểm của AB và MD, H là giao điểm của AD và MC. Chứng minh rằng ba đường thẳng AM, BD, HK đồng quy.
Hướng dẫn giải
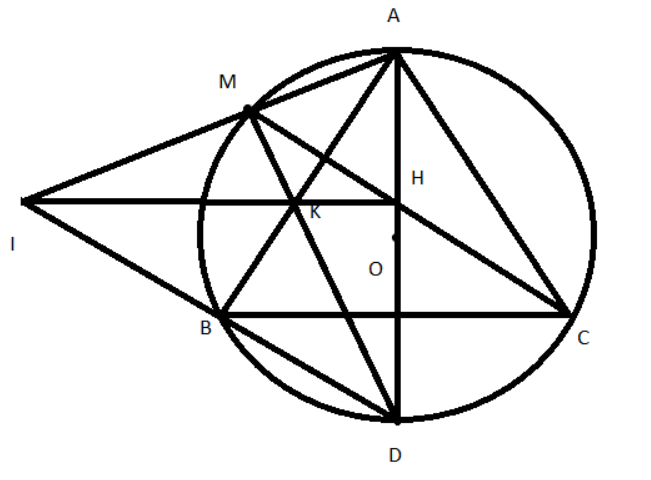
+ Gọi I là giao điểm của AM và DB
+ Có (2 góc nội tiếp đường tròn đường kính AD)
Suy ra AB và DM là hai đường cao của tam giác IAD
K là trực tâm của tam giác nên IK vuông góc với AD (1)
+ Có (tam giác ABC đều) nên hai cung AC và AB bằng nhau
Góc kề bù với góc nên
Suy ra tứ giác IMHD là tứ giác nội tiếp đường tròn đường kính ID
Suy ra IH vuông góc với
Từ (1) và (2) suy ra I, H, K thẳng hàng
Hay ba đường thẳng và HK đồng quy ra I
C. Bài tập tự luyện
Bài 1: Cho tam giác ABC vuông tại A trên cạnh AC lấy M vẽ đường tròn đường kính MC tâm O. Đường thẳng BM cắt đường tròn O tại D. Đường thẳng AD cắt đường tròn O tại S. Gọi E là giao điểm của BC của đường tròn O. Chứng minh: BA , EM , CD đồng quy
Bài 2: Cho nửa đường tròn O, đường kính AB = R, bán kính OC vuông góc AB. M là một điểm trên cung nhỏ BC, AM cắt CO tại N
a) Chứng minh tứ giác BMN nội tiếp đường tròn
b) Chứng minh AM.AN = 2R2
c) Kéo dài BN cắt nửa đường tròn tại K.Chứng minh ba đường thẳng AC, BM, ON đồng quy
Bài 3: Cho nửa đường tròn tâm O đường kính AB. Từ A, B vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Từ M là điểm trên nửa đường tròn (O) (M không là điểm chính giữa cung AB) vẽ tiếp tuyến lần lượt cắt Ax, By tại điểm C, D.
a) Chứng tỏ AC + BD = CD
b) Chứng minh tam giác COD vuông
c) Tia BM cắt Ax tại P, tia AM cắt By tại Q. Chứng minh ba đường thẳng AB, CD, PQ đồng quy.
Bài 4: Cho tam giác ABC vuông ở A. 1 điểm D nằm giữa A và B, đường tròn đường kính BD cắt BC tại E. Các đường thẳng CD, AE cắt đường tròn tại F, G. Chứng minh:
a, Hai tam giác ABC và EBD đồng dạng với nhau
b, Tứ giác ADEC và tứ giác AFBC nội tiếp đường tròn
c, AC // FG
d, Các đường thẳng AC, DE và BF đồng quy

