MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
I. LÝ THUYẾT
1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
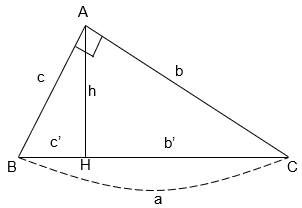
Định lí 1:
Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền:
2. Một số hệ thức liên quan đến đường cao
Định lí 2:
Trong một tam giác vuông bình phương đường cao ứng với cạnh huyền, bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền
Định lí 3:
Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng
Định lí 4:
Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông
II. BÀI TẬP VẬN DỤNG
Bài 1: Hãy tính x, y trong các hình dưới đây:
Bài 2. Cho vuông tại A, đường cao AH = 24cm. Biết AB : AC = 3 : 4. Tính BH, CH
Bài 3. Cho vuông tại A, đường cao AH = 24cm. Biết AB = 7cm; AC = 24cm. Tính BH, CH, AH.
Bài 4. Cho vuông tại A, đường cao AH = 24cm. Biết BH : HC = 9 : 16; AH = 48cm. Tính AB, AC, BC.
Bài 5. Cho vuông tại A, phân giác AD. Biết BD = 3cm; DC = 4cm. Tính BC, AB, AC
Bài 6. Cho tam giác ABC vuông tại A, phân giác BD. Biết AD =4cm, DC =5cm. Tính AB, BC.
Bài 7. Cho tam giác ABC vuông tại A. Đường cao AH. Biết AB :AC= 3:7, AH=42cm. Tính HB, HC.
Bài 8. Cho tam giác ABC vuông tại A, đường cao AH, phân giác AD, biết . Tính HB, HC.
Bài 9. Cho tam giác ABC cân tại A, đường cao AH, BK.
Chứng minh rằng:
Bài 10. Cho tam giác ABC có AB= 6cm, AC =8cm, BC =10cm.
a) Chứng minh tam giác ABC vuông
b) Tính đường cao AH.
Bài 11. Cho tam giác ABC vuông ở A. Biết AB :AC =3 :4, AC =10cm. Tính AB; BC.
Bài 12. Cho tam giác ABC có AB =12cm, AC =16cm, BC =20cm.
a) Chứng minh tam giác ABC vuông
b) Tính đường cao AH
c) Kẻ HD và HE lần lượt vuông góc với AB và AC. Tính HD, HE.
Bài 13. Cho hình chữ nhật ABCD có AB =8cm, BC =15cm.
a) Tính BD
b) Vẽ AH vuông góc với BD tại H. Tính AH.
c) Đường thẳng AH cắt BC ở I, cắt DC tại K. Chứng minh HA2 = HI. HK
Bài 14. Cho hình vuông ABCD, điểm M trên BC, AM cắt DC tại I, AK vuông góc với AI, K thuộc đường thẳng CD. Chứng minh:
a) Tam giác AKM cân.
b)
Bài 15. Cho tam giác ABC vuông tại A. Biết rằng , đường cao AH = 30cm. Tính HB, HC.
Bài 16. Cho tam giác ABC vuông tại A, cạnh AB = 6cm, AC = 6cm. Đường phân giác trong và ngoài của góc C cắt cạnh AC lần lượt tại M và N. Tính độ dài đoạn thẳng AM và AN.
Bài 17. Cho tam giác ABC có trung tuyến AM, đường cao AH. Cho biết điểm H nằm giữa hai điểm B và M, AB = 15cm, AH = 12cm, HC = 16cm.
a) Tính độ dài đoạn thẳng BH, AC.
b) Chứng tỏ tam giác ABC là tam giác vuông. Tính độ dài AM.
Bài 18. Cho tam giác ABC vuông tại A, hai đường trung tuyến AM và BN vuông góc với nhau. Biết BC = 12a. Tính AB và AC.
Bài 19. Cho tam giác ABC có AB = 6 cm, BC = 10 cm và góc ABC = 120o. Kẻ đường cao AH.
a) Tính BH, AH và AC.
b) Lấy điểm M trên đoạn BC với CM = x. Đường song song với AB kẻ từ M cắt AC tại N.

